Условия совпадения повторных и двойных пределов

Теорема. Если 1) существует (конечный или нет) двойной предел А=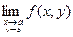

и 2) при любом у из У существует (конечный) простой предел по х

y(y)=

То существует повторный предел n= =

И равен двойному.

Доказательство. Докажем для конечных А,а,b.

Согласно определению предела, по заданному e>0 найдется такое d>0, что

|f(x,y)-A|<e, (*)

лишь только |x-a|<d и |y-b|<d (причем х берется из Х, а у из У).

Фиксируем теперь у так, чтобы выполнялось неравенство |y-b|<d и перейдем в (*) к пределу при х®а.

Т.к. в виду 2), f(x,y) при этом стремится к пределу y(y), то получим

|y(y)-А|£e

Т.к. у – любое число из У, удовлетворяющее условию |y-b|<d, приходим к выводу

А= = . Ч.т.д.

Если, наряду с условиями 1) и 2), при любом х из Х существует (конечный) простой предел по у: =j(х),

то, как следует из доказанного, если х и у поменять ролями, - существует также и второй повторный предел:

m= =

и равен тому же числу А: в этом случае оба повторных предела равны.

Непрерывность функции нескольких переменных.

Определение 1. Пусть функция u=f(M) определена на множестве EÌRⁿ. Пусть А – предельная точка множества Е и АÎЕ. Функция u=f(M) называется непрерывной в точке А, если 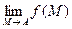=f(A) (1)

Определение 2. (на языке последовательностей). Функция u=f(M) называется непрерывной в точке А, если для любой последовательностей точек {M_k}_kÎN такой, что M_kÎЕ и M_k®A при k®¥ оказывается, что соответствующая последовательность значений функции {f(M_k)}_kÎN имеет своим пределом f(A).

Определение 3. (на языке e и d). Функция u=f(M) называется непрерывной в точке А, если "e>0 $d>0 такое, что при MÎE и r(M,A)<d (расписать покоординатно, т.е. |х₁- |<d,…, |х_n- |<d) Þ|f(M)-f(A)|<e.

Соотношение (1) равносильно следующему:

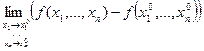=0 (1¢)

Здесь М(x₁,…,x_n), A(,…, ).

Если ввести обозначения Dx₁=x₁- ,…,Dx_n=x_n- , Du=f(x₁,…,x_n)-f(,…, ), то (1¢) пример вид:

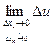=0 (2)

Dx₁,…,Dx_n- приращения независимых переменных, Du – приращение функции.

Т.о. функция u=f(x₁,…,x_n) непрерывна в точке (,…, ) тогда и только тогда, когда приращение функции Du®0, как только стремятся к нулю приращения независимых переменных.

Если положить r= 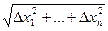, то равенство (2) примет вид: 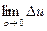=0.

Величина r представляет собой расстояние между точкой (,…, ) и точкой ( +Dx₁,…, +Dx_n).

Если функция u=f(M) непрерывна в каждой точке множества Е, то ее называют непрерывной на множестве Е.

Введенное понятие непрерывности функции u=f(M) в точке А называют непрерывностью этой функции в точке А по совокупности переменных.

Вводится также понятие непрерывности функции u=f(M) в точке А по каждой переменной в отдельности.

Например при n=2. Пусть функция u=f(x,y) определена в некотором прямоугольнике Р, содержащем точку A(a,b). Рассмотрим отрезок прямой х=а, содержащий точку А(а,b) и содержащийся в Р. Рассмотрим функцию u=f(х,y) в точках этого отрезка. Получим функцию u=f(а,y) одной переменной у. Если f(а,y) непрерывна в точке у=b, т.е. если 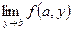=f(a,b), то функция f(x,y) непрерывна в точке A(a,b) по переменной у.

Рассмотрим теперь отрезок прямой у=b, содержащий точку А(а,b) и содержащийся в Р. Рассмотрим функцию u=f(х,y) в точках этого отрезка. Получим функцию u=f(x,b) одной переменной x. Если f(x,b) непрерывна в точке x=a, т.е. если 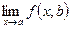=f(a,b), то функция f(x,y) непрерывна в точке A(a,b) по переменной x.

Непрерывность функции u=f(x,y) в точке A(a,b) по совокупности переменных означает, что значение f(x,y) стремится к значению f(a,b), когда точка (х,у) стремится к точке (a,b) с любой стороны и, в частности, вдоль параллели оси Оу или Оси Ох. Следовательно, будут справедливы равенства 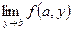=f(a,b) и 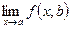=f(a,b).

Т.о., функция f(x,y), непрерывная в точке A(a,b) по совокупности переменных, будет непрерывна в этой точке и по каждой переменой в отдельности.

Но из непрерывности по каждой переменной в отдельности не следует непрерывность по совокупности переменных.

Свойства непрерывных функций нескольких переменных.

1. Алгебраическая сумма, произведение, частное непрерывных функций - непрерывна.

2. Непрерывность сложной функции.

Пусть кроме функции u=f(x₁,…,x_n), заданной в множестве Е n-мерных точек M(x₁,…,x_n), нам даны еще n функций

x₁=j₁(t₁,..,t_m),…,x_n=j_n(t₁,..,t_m) (2)

в некотором множестве F m-мерных точек P(t₁,…,t_m), причем точка М с координатами (2) не выходит за пределы множества Е.

Теорема. Если функции j_i(P) (i=1,2,..,n) все непрерывны в точке P¢(t¢₁,…,t¢_m) из F, а функция f(M) непрерывна в соответствующей точке M¢(x¢₁,…,x¢_n) с координатами

x¢₁=j₁(t¢₁,..,t¢_m),…,x¢_n=j_n(t¢₁,..,t¢_m),

то и сложная функция u=f(j₁(t₁,..,t_m),…,j_n(t₁,..,t_m))=f(j₁(P),…,j_n(P)) будет непрерывна в точке P¢.

Доказательство. Сначала по

 

 

Теорема (аналогичная 1-й теореме Больцано-Коши для функции одной переменной). Пусть функция f(x,y) определена и непрерывна в некоторой связной области D. Если в двух точках М₁(x₁,y₁) и М₂(x₂,y₂) этой области функция принимает значения разных знаков f(x₁,y₁)<0 и f(x₂,y₂)>0, то в этой области найдется такая точка М₀(x₀,y₀), в которой функция обращается в ноль: f(x₀,y₀)=0.

Первая теорема Вейерштрасса. Если функция f(x,y) определена и непрерывна в ограниченной и замкнутой области D (может быть и несвязной), то функция ограничена, т.е. все ее значения содержатся между двумя конечными границами:

m£f(x,y)£M.

Доказательство. Допустим функция f(x,y) неограниченна в D. Тогда "n в D $ точка М_n(x_n,y_n) такая, что |f(x_n,y_n)|>n (3)

Из ограниченной последовательности {M_n} можно извлечь подпоследовательность 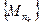, сходящуюся к предельной точке ().

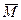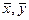Точка 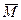ÎD (в противном случае, все точки 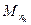были бы от нее отличны, и точка 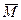была бы точкой сгущения области D ей не принадлежащей, что невозможно в силу замкнутости D.

Вследствие непрерывности функции в точке 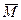должно быть:

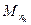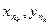f()=f(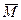)®f()=f(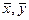). А это противоречит (3) ч.т.д.

Вторая теорема Вейерштрасса. Если функция f(М) определена и непрерывна в ограниченной и замкнутой области D, то она достигает на нем своих наибольшего и наименьшего значений.

Равномерная непрерывность.

Определение. Пусть функция f(М) определена на множестве EÌRⁿ. Функцию f(М) называют равномерно непрерывной на Е, если

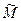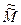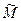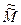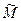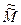"e>0 $d=d(e)>0 такое, что " точек и ÎE для которых r(, )<d Þ|f()-f()|<e.

Или если

"e>0 $d=d(e)>0 такое, что " точек (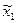,…, 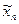) и(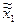,…, 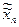) ÎE для которых

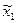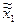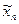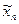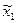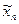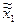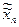| - |<d,…, | - |<d Þ|f(,…, )-f(,…, )|<e.

Теорема Кантора. Если функция f(М) определена и непрерывна на ограниченном замкнутом множестве EÌRⁿ, то она и равномерно непрерывна на этом множестве.