1) множества Rn и Æ - замкнутые (т.к. их дополнения Æ и Rn – открытые).
2) Пересечение любой системы замкнутых множеств – замкнуто (показать).
3) Объединение конечной системы замкнутых множеств – замкнуто (показать).
Классификация точек относительно множества.
Определение. Точка М(x1,…,xn) называется предельной точкой множества ЕÌRn, если в любой окрестности этой точки содержится бесконечно много точек из множества Е.
Множество Е в объединении со множеством своих предельных точек называется замыканием множества Е - 
.
Например, замыкание интервала – отрезок: 
=[a,b].
Если точка М не является предельной для множества Е, то возможно:
1) МÏЕ, то существует шар с центром в точке М, который не содержит ни одной точки из Е.
2) МÎЕ, то существует шар с центром в точке М, который содержит только одну точку Е – точку М.
Теорема. Для того, чтобы множество было замкнутым, необходимо и достаточно, чтобы оно содержало все свои предельные точки.
Определение. Точка М называется внутренней точкой множества Е, если существует окрестность этой точки, входящая в множество Е: $ В(М,R)ÌЕ (только если МÎЕ)
Совокупность всех внутренних точек Е называется внутренностью М.
Точка М называется внешней точкой множества Е, если В(М,R)ÇЕ=Æ (МÏЕ)
Последовательность в Rn.
Пусть {Xk(
,…, 
}, kÎN – некоторая последовательность из Rn.
А(a1,…,an)ÎRn – фиксированная точка.
Определение. Последовательность {Xk} сходится к точке А при k®¥, если
d(X(k),A)®0 при k®¥, (3)
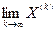=А, X(k)®А, k®¥,
Или последовательность {Xk} сходится к точке А при k®¥, если
" окрестности В(А,R) $N: "n³N Þ X(n)ÎВ(A,R).
Пример. X(k)=(
,0,..,0,1)®А(0,…,0,1) при k®¥.
d(X(k),A)= 
®0, при k®¥.
Свойства сходящихся последовательностей.
1) Сходящаяся последовательность не может иметь более одного предела.
Доказательство. Допустим, что последовательность {Xk} имеет два предела:
X(k)®А, k®¥ и X(k)®В, k®¥,
Тогда по неравенству треугольника: d(A,B)£d(A, X(k))+d(X(k),B)
d(X(k),A)®0, k®¥, d(X(k),B)®0, k®¥.
Т.е. d(A,B)£0Þ d(A,B)=0ÞА=В. Ч.т.д.
2) Если последовательность точек пространства Rn сходится, то она ограничена.
Доказательство. Пусть X(k)®А, k®¥, т.е. d(X(k),A)®0, k®¥. Тогда последовательность {d(X(k),A)} ограничена в силу свойств числовых последовательностей (одномерных), т.е. $С: "k Þ d(X(k),A)£C, т.е. X(k)ÎВ(А,С), т.е. X(k) – ограничена. Ч.т.д.
Связь сходимости последовательностей точек из Rn со сходимостью последовательностей их координат.
Пусть последовательность {x(k)}ÎRn, тогда x(k)=(,…, ), т.е.
x(1)=(
,…, 
), x(2)=(
,…, 
),…
Теорема. Для того, чтобы последовательность точек из Rn сходилась к точке А(a1,…,an), необходимо и достаточно, чтобы сходились все числовые последовательности, составленные из координат этих точек, т.е.
®a1, k®¥,…, ®an, k®¥ (4)
Доказательство. Необходимость. Пусть x(k)®А, k®¥ Ûd(x(k),A)®0, k®¥Û
Û 
®0, k®¥ (5)
Имеем: 0£ê -а1ê£ ,
0£ê 
-а2ê£ ,…,
0£ê -anê£ ,
С учетом (5), получаем, что ®a1, k®¥,…, ®an, k®¥.
Достаточность. Пусть ®a1, k®¥,…, ®an, k®¥. Тогда
( -a1)®0, k®¥,…,( -an)®0, k®¥ Þ ( -a1)2®0, k®¥,…,( -an)2®0, k®¥
Þ(( -a1)2+…+( -an)2)®0, k®¥Þ d(x(k),A)®0, k®¥Þ x(k)®А, k®¥. ч.т.д.
Определение. Последовательность {x(k)}ÎRn называется фундаментальной, если d(x(k),x(m))®0, k,m®¥ (6)
Теорема. Для того, чтобы последовательность {x(k)} из Rn сходилась, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство. (Показать, что {x(k)} фундаментальная Û когда фундаментальны последовательности ее координат.)
Теорема.. Из всякой ограниченной последовательности точек {x(k)} из Rn можно извлечь сходящуюся подпоследовательность.
Доказательство. Пусть последовательность {x(k)} ограничена, тогда
$C>0: "k=1,2,… и "i=1,2,..,n Þ ê 
ê£CÞограничены последовательности всех координат.
Докажем для случая n=2. Т.е. для последовательности {x(k)(xk,yk)}.
Тогда последовательности {xk}kÎN и {уk}kÎN – ограничены.
Рассмотрим последовательность {xk}kÎN – она числовая и ограниченная. Следовательно (по принципу Больцано-Вейерштрасса) из нее можно извлечь сходящуюся подпоследовательность. Пусть это будет подпоследовательность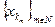 
и пусть 
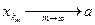(а – конечное число).
Из последовательности {уk}kÎN выделим подпоследовательность 
так, чтобы индексы этой подпоследовательности совпадали с индексами подпоследовательности .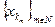
Подпоследовательность - числовая, ограниченная. Поэтому из нее можно извлечь сходящуюся подпоследовательность. Пусть это будет подпоследовательность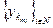 
. Пусть 
(b – конечное число).
Теперь из 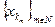выделим подпоследовательность 
так, чтобы ее индексы совпадали с индексами 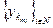. Тогда 
(т.к. любая подпоследовательность, выделенная из сходящейся последовательности, сходится к тому же пределу).
Т.о. 
= 
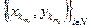- искомая последовательность, которая сходится к точке А(a,b). Ч.т.д.
Определение. Множество МÌRn называется компактным, если из любой последовательности точек из М можно выделить сходящуюся подпоследовательность, предел которой лежит в М.
Примеры. Отрезок – компактное множество, а интервал и полуинтервалы – нет (последовательность может сходится к концу интервала, который ему не принадлежит).
Теорема. Для того, чтобы множество МÌRn было компактным, необходимо и достаточно, чтобы оно было замкнутым и ограниченным.
Понятие функции нескольких переменных.
Пусть имеется множество Е пар чисел (х,у). Геометрически Е представляет собой некоторое множество точек плоскости Оху.
Если каждой точке (х,у)ÎЕ по какому-либо правилу сопоставить определенное значение переменной z, то говорят, что на множестве Е задана функция z=f(x,y).
Переменные х и у называют независимыми переменными или аргументами, а множество Е – областью определения функции.
Геометрически функция z=f(x,y) иллюстрируется следующим образом. Рассмотрим прямоугольную систему координат Охуz и предположим, для простоты, что область задания Е функции представляет собой часть плоскости Оху. Возьмем на Е какую-нибудь точку М(х,у) и вычислим соответствующее значение z. Это значение z отложим на перпендикуляре к плоскости Оху, проходящем через точку М(х,у). В результате получим в пространстве точку Р(х,у,z). Когда точка М(х,у) будет перемещаться в области задания Е, соответствующая точка Р(х,у,z) опишет, как правило, некоторую поверхность. Эта поверхность служит геометрическим изображением данной функции z=f(x,y). Т.о. графиком функции двух переменных z=f(x,y) называется множество точек трехмерного пространства (х,у,z), аппликата z которых связана с абсциссой х и ординатой у соотношением z=f(x,y).
График функции z=f(х1,х2,…,хn) имеет геометрическую интерпретацию только при n≤2. n=1 - линия на плоскости Оху, n=2 – поверхность в пространстве R3.
Определение. Функцией n переменных называется закон, правило, по которому каждому набору из n переменных (х1,х2,…,хn) из некоторого множества Х ставится в соответствие единственное значение переменной u.
u=f(х1,х2,…,хn)
Переменные х1,х2,…,хn – называются независимыми или аргументами, переменная u – зависимой. Если точку (х1,х2,…,хn) обозначить через М, то функцию u=f(х1,х2,…,хn) называют функцией точки М и обозначают u=f(М).
Областью определения функции z называется множество значений переменных х1,х2,…,хn при которых функция имеет смысл. (множество Х 
Rn).
Геометрическая интерпретация ООФ возможна только при n≤3.
n=1 функция одной переменной, ООФ – некоторый промежуток прямой Ох.
n=2 функция двух переменных, ООФ – часть (или вся) плоскости Оху.
n=3 функция трех переменных, ООФ – часть или все пространство R3.
Пример. Найти ООФ z=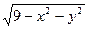 
.
1-х2-у2≥0, х2+у2≤1
Все точки М(х,у), удовлетворяющие этому неравенству, лежат в круге радиуса 3 с центром в (0;0) и на границе этого круга (рисунок).
Предел функции нескольких переменных.
Пусть функция u=f(М) определена на множестве ЕÌRn. Пусть точка М0 – предельная точка множества Е.
Определение 1. Функция u=f(х1,х2,…,хn) имеет пределом число А при стремлении переменных х1,х2,…,хn, соответственно, к а1,а2,…,аn, если
"e>0 $d>0: êx1-a1ê<d,….,êxn-anê<dÞêf(х1,х2,…,хn)-Aê<e
При этом точка М(х1,…,хn) предполагается взятой из Е и отлична от М0(а1,…,аn).
Т.о. неравенство должно выполняться во всех точках множества Е, лежащих в достаточно малой окрестности точки М0: (а1-d,а1+d;…;аn-d,аn+d), но исключая саму точку М0 (если М0ÎЕ).
А= 
или А= 
Например, при n=2. Число А называется пределом функции z=f(x,y) при х→х0, у→у0 (в точке (х0,у0)), если для любого, сколь угодно малого положительного числа ε>0, найдется положительное число δ>0, зависящее от ε, δ=δ(ε)), такое, что для всех точек (х,у), отстоящих от точки (х0,у0) на расстояние 0<ρ<δ, выполняется неравенство
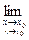f(x,y)=А
(
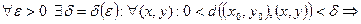
Определение 2. Число А называется пределом функции f(М) при М®М0, если
"e>0 $d>0 такое, что как только МÎЕ, М¹М0 и d(M,M0)<dÞêf(M)-M0ê<e
Определение 3. Функция u=f(х1,х2,…,хn) имеет пределом число А при стремлении переменных х1,х2,…,хn, соответственно, к а1,а2,…,аn, если для любой последовательности точек {Mk}kÎN такой, что
"kÎN, MkÎE, Mk¹M0 и Mk®M0 при k®¥ соответствующая последовательность значений функции f(M1),…,f(Mk),… всегда имеет одно и то же число A.
Пример.
