Функции нескольких переменных.
При изучении многих явлений приходится встречаться с функциями двух и более независимых переменных.
Примеры.
1) Площадь прямоугольника со сторонами х и у: S=xy.
2) Объем прямоугольного параллелепипеда с ребрами x,y,z: V=xyz.
3) По закону Ома, напряжение U в цепи электрического тока связано с сопротивлением R цепи и силой тока I зависимостью U=RI. Если считать U и R данными, то I определится как функция от U и R: I= 
.
Элементами арифметического пространства Rn являются упорядоченные наборы из n действительных чисел (х1,х2,…,хn). Эти упорядоченные наборы называются точками n-мерного пространства или n-мерными векторами.
х=(х1,х2,…,хn), у=(у1,у2,…,уn). х1,х2,…,хn – координаты точки.
Определение. Расстояние между точками х=(х1,х2,…,хn) и у=(у1,у2,…,уn):
d(x,y)= 
(1)
Свойства расстояния:
1) d(x,y)³0, причем, d(x,y)=0 Û х=у, т.е. xi=yi "i=1,2,…,n.
2) d(x,y)=d(y,x) – свойство симметрии.
3) d(x,y)£d(x,z)+d(z,y) "x,y,zÎRn – неравенство треугольника (
£ 
+ 
).
Пусть a(а1,а2,…,аn) – произвольная точка пространства Rn и пусть R>0 – некоторое число. Множество всех точек x(х1,х2,…,хn):
В(a,R)={xÎRn: d(x,a)<R} - открытый шар (сфера) с центром в точке а и радиуса R.
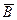(a,R)={xÎRn: d(x,a)£R} – замкнутый шар (сфера) с центром в точке а и радиуса R.
S(a,R)={xÎRn: d(x,a)=R} – сфера в Rn.
Следовательно, уравнение сферы в Rn:
=R (2)
Определение. Пусть имеются числа a1,…,an и b1,…,bn такие, что a1<b1,…,an<bn. Множество всех точек M(х1,х2,…,хn)ÎRn, для которых
называют открытым параллелепипедом – Р.
Множество всех точек M(х1,х2,…,хn)ÎRn, для которых
называют закрытым параллелепипедом –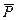 
.
Точка С(
,…, 
) – центр параллелепипеда.
Открытую сферу любого радиуса R>0 с центром в точке М0(
,…, 
) можно рассматривать как окрестность этой точки. (Аналогично, в качестве окрестности можно рассматривать открытый параллелепипед с центром в точке М0(,…, )).
Определение. Пусть Е – некоторое множество точек из Rn. Множество Е называется ограниченным, если существует число R>0 такое, что все точки множества Е оказываются лежащими внутри сферы радиуса R с центром в точке О(0,…,0).
Теорема. Пусть множество Е(М)ÌRn. Пусть
{x1} - множество, которое образуют первые координаты точек МÎЕ,
…………………………………………………………………………..
{xn} - множество, которое образуют n-е координаты точек МÎЕ.
Для того, чтобы множество Е(М) было ограниченным необходимо и достаточно, чтобы были ограниченными одновременно множества {x1},..., {xn}.
Доказательство. Необходимость. Пусть Е(М) – ограниченное. Следовательно, существует число R>0 такое, что d(M,O)<R "M(x1,…,xn)ÎE. Тогда имеем
0£êx1ê£ 
<R, …, 0£êxnê£ <R "M(x1,…,xn)ÎE
А это и означает, что множества {x1},..., {xn} ограничены.
Достаточность. Пусть множества {x1},..., {xn} – ограниченные. Следовательно, $С>0: êx1ê<C, …,êxnê<C "M(x1,…,xn)ÎE. Тогда <C 
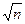=R
т.е., d(M,O)<R "MÎE. А это означает, что множество Е – ограниченное. ч.т.д.
Определение. Множество называется открытым, если каждая точка этого множества входит в него вместе со своей окрестностью.
Свойства открытых множеств.
1) множества Rn и Æ - открытые.
2) Объединение любой системы открытых множеств – открыто (показать).
3) Пересечение конечной системы открытых множеств – открыто (показать).
Точка М0ÎЕ называется точкой сгущения множества ЕÌRn, если в каждой ее окрестности содержится хотя бы одна точка множества Е, отличная от М0.
Определение. Множество FÌRn называется замкнутым, если его дополнение в Rn открыто (т.е. если Rn\F – открыто).
Точки сгущения открытого множества, не принадлежащие ему, называются пограничными точками этого множества. Пограничные точки образуют границу множества.
Открытое множество со своей границей называется замкнутым.
