2) 
= 
= 
= 
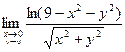=0
сделаем замену t= 
, t→0 при x→0, y→0
Замечание. Для функции f(х1,х2,…,хn) нескольких переменных, как и для функции одной переменной, можно ввести понятие бесконечного предела, а также понятие предела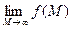 
, когда точка неограниченно удаляется от начала координа, т.е. когда 
®+¥.
Бесконечно малые и бесконечно большие вводятся так же, как и в случае функции одной переменной.
Определение. Функция f(М) называется бесконечно малой при М®М0, если
=0.
Функция f(М) называется бесконечно большой при М®М0, если
=¥, +¥, -¥.
Свойства бесконечно малых и бесконечно больших функций, установленные для случая функций одной переменой, распространяются на случай функции нескольких переменных. Сохраняются так же понятия порядка, эквивалентности бесконечно малых и бесконечно больших и свойства, связанные с этими понятиями.
Сохраняются и свойства конечных пределов.
1. Число А является пределом функции f(М) при М®М0 тогда и только тогда, когда разность f(М)-М0 есть бесконечно малая при М®М0.
Или число А является пределом функции f(М) при М®М0 тогда и только тогда, когда f(М)=А+a(х1,х2,…,хn), где a(х1,х2,…,хn) – б.м. при М®М0.
2. если существует конечный предел , то при любом постоянной С существует конечный предел 
, причем
=С×
3. Если существуют конечные пределы и 
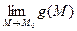, то существует и конечный предел 
, причем
= ±
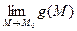
Это свойство распространяется на любое фиксированное число слагаемых.
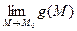4. Если существуют конечные пределы и , то существует и конечный предел 
, причем
= ×
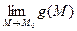
Это свойство распространяется на любое фиксированное число сомножителей.
5. Если существуют конечные пределы и 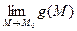, причем 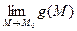¹0, то существует конечный предел 
, причем
= 
6. Если в некоторой окрестности точки М0 р(М)£f(M)£g(M) и если 
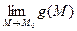= =А, то и =А.
Повторные пределы.
Кроме рассмотренного предела функции f(х1,х2,…,хn) при одновременном стремлении всех аргументов к их пределам, рассматриваются пределы, получаемые в результате ряда последовательных предельных переходов по каждому аргументу в отдельности в том или ином порядке. Первый предел называется n-кратным (двойным, тройным и т.д. при n=2,3,..), а последний – повторным.
Рассмотрим функцию двух переменных f(х,у).
Допустим, что область изменения переменных х и у такова, что х (независимо от у) может принимать любое значение в некотором множестве Х, для которого а служит точкой сгущения, но ему не принадлежит, и аналогично у (независимо от х) изменяется в множестве У с не принадлежащей ему точкой сгущения b. Такую область можно символически обозначить как Х´У.
Пусть, например, она задана в прямоугольнике (Р)=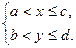 
. Пусть при каждом фиксированном х из (a,c] существует конечный предел 
. Предел будет представлять собой функцию от х, определенную в промежутке (a,c], т.е.
=j(х), хÎ(a,c].
Пусть существует конечный предел m= 
. Число m называют повторным пределом функции f(х,у) в точке А(а,b):
m= 
Пусть при каждом фиксированном y из (b,d] существует конечный предел 
. Предел будет представлять собой функцию от y, определенную в промежутке (b,d], т.е.
=y(y), yÎ(b,d].
Пусть существует конечный предел n= 
. Число n будет другим повторным пределом функции f(х,у) в точке А(а,b):
n= 
Пример. Для функции f(x,y)= 
в точке О(0,0) найти повторные пределы и доказать, что у этой функции в точке О(0,0) нет двукратного предела.
1) При фиксированном х¹0 имеем:
= 
=1, т.е. jº1, хÎ(-¥;0)È(0;+¥). Тогда
= 
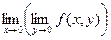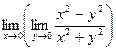=1, т.е. m=1.
2) При фиксированном у¹0 имеем:
= 
=-1, т.е. yº-1, уÎ(-¥;0)È(0;+¥). Тогда
= 
=-1, т.е. n=-1.
Т.о., в точке (0,0) существуют оба повторных предела и m¹n.
3) Покажем, что в точке (0,0) не существует предела в обычном смысле.
Возьмем последовательность точек 
. "kÎN точки Mk 
принадлежат области существования функции, ¹(0,0), и Mk ®О(0,0) при k®¥.
Соответствующая последовательность значений функции будет такой: f(M1)=0, f(M2)=0,…,f(Mk)=0,…. Следовательно, f(Mk)®0, при k®¥.
Возьмем последовательность точек 
"kÎN точки 
принадлежат области существования функции, ¹(0,0), и ®О(0,0) при k®¥.
Соответствующая последовательность значений функции будет такой: f(
)= 
, f(
)= ,…,f()= ,…. Следовательно, f()® , при k®¥.
Следовательно, предела в обычном смысле нет.
