Многогранником называется сплошное тело, у которого плоские ограничивающие грани являются полигонами. Если все стороны полигона имеют одинаковую длину, а все внутренние углы равны между собой, то такой полигон называется правильным. Многогранник называется правильным, если его полигоны правильны. Существует всего пять правильных многоугольников, называемых платоновыми телами.
Платоновы тела
Платоново тело есть тело наименьшей поверхности при заданном объеме, состоящее из одинаковых фигур (простейших). Правильный многоугольник ограничивает собой объем больший, чем любое тело с тем же числом граней.
Пара цифр, записанная в скобках через запятую рядом с названием каждой фигуры, называется "символом Шлефли", трактуются эти цифры так: (<число вершин одной грани фигуры>, <число сходящихся в одной вершине граней>).

| 
| 
|
| Тетраэдр (3, 3) | Куб (4, 3) | Октаэдр (3, 4) |

| 
| |
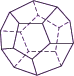
| Икосаэдр (3, 5) | Додекаэдр (5, 3) |
Существуют две пары фигур, имеющих в символе Шлефли две одинаковые цифры, которые различаются только порядком следования. Вот эти пары: "куб"-"октаэдр" и "икосаэдр"-"додекаэдр". Они обладают интересным свойством: вершины одной парной фигуры размещаются точно в серединах граней другой парной фигуры.
В трехмерном пространстве тетраэдр является симплексом (простейшей фигурой) и обращается сам в себя, то есть парой тетраэдру будет он сам.
На плоскости существует только три правильных многоугольника, которые дают укладку без разрывов (100% укладку) - это квадрат, равносторонний треугольник и шестиугольник. Другие правильные многоугольники не дают 100% укладки. Обратите внимание: 100% укладку можно получить и с использованием неправильных многоугольников, яркий тому пример - картина Эшера.

| 
| 
|
| Решетка (4, 4) | Мозайка (3, 6) | Соты (6, 3) |
Психофизиологические аспекты восприятия пространства и воспроизведения его на плоскости
Иллюзии
Мы познаем мир логически, мы часто видим не то, что есть на самом деле; создаются иллюзии, зрение обманывает нас. Поэтому только анализируя сигналы, поступающие в наш мозг из окружающего нас мира, мы получаем реальное представление о нем. Обычно человек смотрит на мир с высоты своего роста, мы видим, что чем дальше от нас предмет, тем он меньше и наоборот.
Вот несколько распространенных примеров иллюзий.
Сад Рэндзю - доказательство постижения сути (пространства, явлений) путем логического мышления. Сад представляет собой прямоугольную площадку 30 метров в длину и 10 - в ширину. На площадке особым образом лежат 15 камней. Можно ходить вдоль линии площадки, но ни с одной точки мы не увидим все 15 камней - только 14. То есть видимость обманчива: не видя всех камней сразу, мы, тем не менее, знаем, что их именно 15, понимая это путем "логических выкладок" нашего мозга.
Другой пример из той же области. Никто никогда не видел одновременно все шесть граней куба, но никто и никогда не спутает куб с тетраэдром или, скажем, со сферой. Почему? Оказывается, при обходе и рассматривании нами куба, наш мозг запоминает его конфигурацию и то, как он выглядит с каждой из сторон. Глядя в следующий раз на куб с одной точки, мы не имеем достаточно информации о нем (мы видим лишь одну, две, или, максимум, три его грани), но наш мозг, помня конфигурацию куба, подсказывает нам, что это именно куб. Таким образом, часто мы логически осознаем (и узнаем) тот или иной предмет.
Круг слева (рис. 20.2) кажется больше круга справа, хотя по построению они одинаковы.

На рис. 20.3 две параллельные линии кажутся непараллельными.

Кажется (рис. 20.4), что верхняя линия короче нижней, а на самом деле они равны.

Кажется (рис. 20.5), что горизонтальные отрезки разной длины, а на самом деле они одинаковы.







