Кривизна - это величина, характеризующая отклонение кривой (поверхности) в окрестности данной ее точки от касательной прямой (касательной плоскости). Понятие кривизны распространяется также и на объекты более общей природы. Например, в римановой геометрии (см. ниже) кривизна представляет собой меру отклонения так называемых римановых пространств от евклидовых.
Кривизна Гаусса
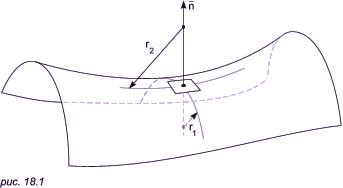
Кривизна Гаусса, или искривленность, обозначается K = k1 * k2, где k1 - наибольшая главная кривизна, k2 - наименьшая главная кривизна, k1 и k2 перпендикулярны друг к другу (см. рис.18.1). Главная кривизна ki = 1/ri. Искривленность К не изменяется при изгибании поверхности, то есть длины и углы кривых на ней остаются неизменными (это значит, что поверхность сделана из абсолютно нерастяжимого материала).
Если для некоторого пространства кривизна Гаусса K = 0, то мы имеем дело с пространством Евклида, в котором справедлива геометрия Евклида. При K > 0 мы переходим к пространству и геометрии Римана, которые имеют свои, отличные от Евклидовой геометрии, законы. А при K < 0 мы приходим к геометрии Лобачевского.
Как было сказано выше, при K = 0 мы имеем дело с привычной всем геометрией Евклида. Пространством этой геометрии является плоскость, на которой выполняются следующие Евклидовы аксиомы
1. сочетания:
· через две точки проходит одна и только одна прямая;
· всякая прямая содержит, по крайней мере, две точки;
· существуют, по крайней мере, три точки, не расположенные на одной и той же прямой;
2. порядка:
· из трех точек, лежащих на одной прямой, одна лежит необходимо между двумя другими;
· для каждых двух точек A и B можно найти по крайней мере одну точку C такую, что она лежит между A и B;
· если прямая пересекает одну сторону некоторого треугольника, то она либо проходит через вершину противоположного угла, либо пересекает еще одну сторону треугольника;
3. конгруэнтности:
· всякий отрезок всегда может быть отложен на прямой по обе стороны от некоторой точки прямой, получающиеся отрезки называются конгруэнтными с первым отрезком;
· если два отрезка конгруэнтны с третьим, то они также конгруэнтны друг с другом;
· если на двух конгруэнтных отрезках имеется по одной такой точке, что одна из получающихся частей одного отрезка конгруэнтна с одной из частей второго отрезка, то и вторая часть первого отрезка конгруэнтна со второй частью второго;
· угол может быть отложен на плоскости по обе стороны от некоторой полупрямой однозначно, получающийся угол называется конгруэнтным с первоначальным;
· если две стороны и угол, заключенный между ними, одного треугольника совпадают с двумя сторонами и углом, заключенным между ними, другого треугольника, то треугольники конгруэнтны;
4. параллельности:
· ко всякой прямой A через всякую не лежащую на этой прямой точку можно провести одну и только одну прямую, не пересекающую прямую A;
5. неперывности:
· всякий отрезок можно измерить при помощи любого другого;
· во всякой последовательности вложенных друг в друга отрезков существет всегда общая всем этим отрезкам точка.
Сумма углов произвольного треугольника, построенного на евклидовой плоскости (рис. 18.2), равна строго 180о.

Рассмотрим теперь геометрию Римана (K > 0). Пространством в этой геометрии является поверхность сферы некоторого радиуса r. Разумеется, на сфере также можно построить треугольник (рис. 18.3), но самое интересное заключается в том, что сумма углов этого треугольника не постоянна и колеблется в пределах от 180o до 270o. Если мы станем непрерывно увеличивать радиус сферы, то стороны треугольника все больше и больше будут спрямляться, углы между его сторонами уменьшаться до некоторой постоянной величины, и при r стремящимся к бесконечности мы придем к геометрии Евклида, в которой, как и полагается, сумма углов треугольника составит 180o. Если же радиус сферы устремить к нулю, углы между любыми двумя сторонами треугольника будут стремиться к 90o и, таким образом, сумма углов треугольника в пределе составит 90o + 90o + 90o = 270o.

В римановой геометрии не выполняются аксиомы Евклида. Возьмем, например, следующую аксиому: "ко всякой прямой A через всякую точку B, не лежащую на этой прямой, можно провести одну и только одну прямую, не пересекающую прямую A". В геометрии Римана на сфере ко всякой прямой A через всякую точку B, не лежащую на этой прямой, можно провести БЕСКОНЕЧНО МНОГО прямых, не пересекающих прямую A, что и иллюстрируется рис. 18.4.

Нам могут возразить, что "бесконечное число прямых" не параллельно прямой A, но ведь аксиома, приведенная выше, и не требует параллельности, она лишь утверждает, что линии не пересекаются, что мы и имеем в данном случае.
Как и в геометрии Римана, в геометрии Лобачевского (K < 0) сумма углов треугольника не постоянна, но теперь она может меняться от 0o до 180o. Если кривизна Гаусса поверхности Лобачевского (рис. 18.5) будет стремиться к нулю, то мы, в конце концов, придем к геометрии Евклида, и сумма углов треугольника составит 180o. Если же кривизна Гаусса будет стремиться к "минус бесконечности", то углы между любыми двумя сторонами треугольника будут становиться все меньше и меньше, и в пределе сумма углов треугольника составит 0o + 0o + 0o = 0o.

Итак, рассмотрев геометрии Евклида, Римана, Лобачевского, можно сделать очень важный вывод о том, что все эти геометрии не живут обособлено, а переходят одна в другую (можно сказать, дополняют друг друга) при изменении некоторых условий.
Как же измерить кривизну интересующего нас пространства? Рассмотрим один из способов. Выясним кривизну пространства Евклида.
Будем проводить окружности с разными радиусами (рис. 18.6, слева) и измерять радиусы и длины каждой полученной окружности, отмечая это на графике (рис. 18.6, справа). При большом числе проведенных окружностей мы получим на графике прямую линию C(R) = 2πR с угловым коэффициентом 2π, а линейной зависимости соответствует кривизна K = 0.

Проведем подобный опыт для сферы (рис. 18.7, слева). Сверху вниз (от точки A до точки B) будем проводить горизонтальные сечения сферы и измерять радиус и длину окружности каждого из полученных сечений. В результате этого эксперимента мы обнаружим, что длина i-ой окружности ci зависит от ее радиуса ri нелинейно (рис. 18.7, справа), поэтому мы с уверенностью можем утверждать, что кривизна K на сфере отлична от нуля.







