Функциональная схема импульсной АСУ приведена на рис. 3.2.
W1(p) и W2(p) – передаточные функции звеньев:
, 
.
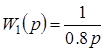Рис. 3.2. Функциональная схема импульсной АСУ:
ОР – объект регулирования, АР – автоматический регулятор
Преобразованная функциональная схема импульсной АСУ с фиксатором нулевого порядка приведена на рис. 3.3.
Рис. 3.3 Преобразованная функциональная схема импульсной АСУ
Передаточная функция фиксатора нулевого порядка: 
.
В результате свертки функциональная схема ИАСУ примет вид (рис. 3.4).
Рис. 3.4. Свернутая функциональная схема АСУ
1.2.1. Запишем передаточную функцию непрерывной части системы:
.
Схема z-модели АСУ имеет вид (рис. 3.5).
Рис. 3.6. Схема z-модели АСУ
1.2.2. Определим z-изображение передаточной функции разомкнутой АСУ:
,
т.к. 
, то
.
Правую часть выражения необходимо представить в виде суммы простых дробей с переменной z в числителе. Разложение можно выполнить методом неопределенных коэффициентов или в пакете Matlab с помощью команды [R,P,K]=residue(B,А).
z-изображение передаточной функции разомкнутой АСУ W(z) может быть получено с помощью следующих команд Control System Toolbox пакета Matlab:
>> W1=tf([1],[0.8 0]);
>> W2=tf([1],[0.8 1]);
>> W=series(W1,W2);
>> Wz=c2d(W,1,'zoh')
Transfer function:
0.5365 z + 0.3554
----------------------
z^2 - 1.287 z + 0.2865
Sampling time: 1 – период дискретизации.
1.2.3. Передаточную функцию замкнутой ИАСУ определим по формуле
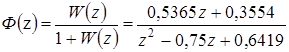
или с помощью функции Control System Toolbox пакета Matlab:
>> Fiz=feedback(Wz,1)
Transfer function:
0.5365 z + 0.3554
---------------------
z^2 - 0.75 z + 0.6419
Sampling time: 1 – период дискретизации.
1.2.4. Найдем z-изображение выходного сигнала:
, т.к. 
для 
.
.
1.2.5. Выходной сигнал можно определить с помощью обратного z-преобразования: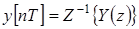 
. Переходная характеристика замкнутой ИАСУ (рис. 3.7) может быть получена с помощью команды step Control System Toolbox пакета Matlab:
>> step(Fiz);grid
Рис. 3.7. Переходная характеристика замкнутой ИАСУ
1.2.6. Моделирование импульсной АСУ может быть также выполнено в Matlab/Simulink. Схема z-модели, рассматриваемой в данном примере, показана на рис. 3.8.
Рис. 3.8. Схема z-модели ИАСУ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Задание и таблица вариантов
Для заданной передаточной функции W0(p) (табл.1) рассчитать W(z), используя метод Z-преобразования.
Выполнить моделирование непрерывного объекта и его дискретной модели, не замыкая систему. Замкнуть систему и сравнить свойства замкнутой непрерывной системы со свойствами замкнутой дискретной системы.
Таблица 1
| Вариант | Параметры | |||||
| W0(p) | T0 | K | T1 | T2 | d | |
| 0.2 | 1.5 | 2.0 | - | - | |
| 0.4 | 3.0 | 1.6 | - | - | ||
| 0.2 | 2.0 | 1.8 | – | – | ||
| 0.3 | 2.5 | 1.5 | – | – | ||
| 0.5 | 3.5 | 2.5 | – | – | ||
| 0.2 | 2.0 | 2.0 | 1.4 | - | |
| 0.3 | 1.2 | 0.8 | 2.5 | - | ||
| 0.4 | 1.0 | 2.5 | 4.0 | - | ||
| 0.5 | 1.5 | 2.2 | 3.0 | – | ||
| 0.3 | 3.0 | 0.5 | 2.0 | – | ||
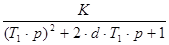
| 0.4 | 1.4 | 2.2 | - | 0.8 | |
| 0.2 | 1.6 | 3.0 | - | 0.7 | ||
| 0.5 | 1.2 | 2.5 | – | 0.5 | ||
| 0.3 | 1.8 | 2.7 | – | 0.6 | ||
| 0.4 | 2.0 | 2.1 | – | 0.4 |
Порядок выполнения работы
2.2.1. Сформировать структурную схему замкнутой импульсной АСУ и привести ее к виду (см. рис. 3.3).
2.2.2. В качестве формирующего звена использовать фиксатор нулевого порядка с передаточной функцией .
2.2.3. Проанализировать устойчивость линейной части системы.
2.2.4. При заданных коэффициентах передаточной функции линейной части системы и заданном периоде дискретизации T0 (см. табл. вар.) найти передаточные функции разомкнутой и замкнутой импульсной системы.
2.2.5. С помощью пакета Matlab/Simulink составить структурную схему замкнутой импульсной АСУ. Выполнить моделирование и получить график переходного процесса. Например, схема ИАСУ и график переходного процесса могут иметь следующий вид (рис. 3.9).
| 
|
Рис. 3.9. Схема моделирования ИАСУ и график переходного процесса
2.2.6. Получить частотную характеристику ИАСУ и определить запас устойчивости с помощью функций bode и margin.
2.2.7. Разомкнуть внешнюю обратную связь и получить амплитудно-фазовую характеристику W*(jw). С помощью частотных критериев оценить устойчивость импульсной системы. Для этого можно применить функцию nyquist Control System Toolbox пакета Matlab:
>> nyquist(W_raz)
Сделать выводы.
2.2.8. Известно, что об устойчивости замкнутой импульсной системы можно судить по расположению полюсов ее передаточной функции в плоскости z относительно окружности единичного радиуса. Условием устойчивости будет нахождение полюсов передаточной функции замкнутой импульсной системы внутри этой окружности. Воспользуйтесь функцией pzmap Control System Toolbox пакета MatLab для того, чтобы оценить расположение корней передаточной функции замкнутой импульсной системы относительно окружности единичного радиуса в плоскости z:
>> pzmap(W_zam)
Сделайте выводы.
2.2.9. По графику переходной характеристики оценить качество ИАСУ: время нарастания, время регулирования, колебательность и перерегулирование.
2.2.10. Исследовать влияние на устойчивость и качество процесса регулирования изменения периода дискредитации Т0 и общего коэффициента передачи системы К.
2.2.11. Путем проведения экспериментов на модели ИАСУ в Matlab/Simulink определить значение периода дискретизации Т0, при котором замкнутая импульсная система будет находиться на границе устойчивости.
Контрольные вопросы
1. Что представляет собой простейший импульсный элемент и формирующее звено?
2. Как образуется приведенная непрерывная часть ИАСУ?
3. Каким образом может быть получена передаточная функция ИАСУ?
4. Опишите метод Z-преобразования.
5. Чем отличаются переходные процессы в замкнутой непрерывной и замкнутой дискретной системах?
6. Как оценить устойчивость импульсной АСУ?
7. Как влияет изменение периода дискретизации на устойчивость и качество импульсной системы?
Лабораторная работа №4
