Основными показателями качества импульсных систем являются время регулирования, перерегулирование, число колебаний, статическая ошибка. Эти показатели определяют по импульсной переходной функции h[nT], являющейся реакцией на единичную дискретную ступенчатую функцию g[nT] = 1 [nT].
Передаточная функция замкнутой системы
 . (1.58)
. (1.58)
Изображение выходной величины
 . (1.59)
. (1.59)
 . (1.60)
. (1.60)
Изображение дискретной переходной функции
 . (1.61)
. (1.61)
Теперь по изображению H(z) надо найти оригинал h[nT], то есть осуществить обратное z -преобразование.
Для этого используют метод разложения функции в степенной ряд по отрицательным степеням. Коэффициенты степенного ряда равны дискретным значениям импульсной переходной функции в моменты времени t = nT, n = 0, 1, 2, ….
Пример. Дана структурная схема импульсной АCУ (рис. 1.47).

Рис. 1.47. Структурная схема импульсной АCУ
Определить показатели качества системы.
Решение.

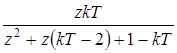 .
.
Пусть, например, kT = 1,5.
Тогда
 .
.
После деления числителя на знаменатель получим степенной ряд
 .
.
Коэффициенты степенного ряда определяют значения функции в дискретные моменты времени
 и т.д.
и т.д.
Рассчитаем значения h[nT] для kT = 1,5; kT = 1 и kT = 0,5. Результаты занесем в таблицу 1.4.
Таблица 1.4
| kT | t = nT | |||||
| 0 | T | 2T | 3T | 4T | 5T | |
| 1,5 | 1,5 | 0,75 | 1,125 | 0,943 | 1,062 | |
| 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | |
| 0,5 | 0,5 | 0,75 | 0,875 | 0,938 | 0,972 |
Построим графики переходных процессов (рис. 1.48) и определим показатели качества.
 |
 
| tp @ 5T s = 50% n @ 2,5 Dy ст ® 0 |
 
| tp @ T s = 0% n = 0 (оптимальный процесс) |

| tp @ 5Т s = 0% n = 0 Dy ст ® 0 |
Рис. 1.48. Графики переходных процессов и показатели качества ИАCУ
Синтез дискретных систем
При синтезе дискретных систем, как и в случае непрерывных систем, необходимо обеспечить требуемые показатели качества управления. В непрерывных системах эта цель достигается включением в контур управления аналоговых регуляторов или корректирующих устройств, при этом определяется их место включения, динамическая структура и параметры. В случае дискретных систем возможности синтеза шире, так как кроме аналоговых регуляторов могут применяться дискретные регуляторы и корректирующие устройства. Также при использовании средств вычислительной техники могут применяться вычислительные алгоритмы коррекции.
Рассмотрим структурные схемы дискретных систем с коррекцией на входе ключа (рис. 1.49) и коррекцией на входе непрерывной части (рис. 1.50): Kk(p) – передаточная функция корректирующего устройства, KФУ(p) – передаточная функция формирователя, KНЧ(p) – передаточная функция непрерывной части САУ.
 |
Рис. 1.49. Структурная схема дискретной системы
с коррекцией на входе ключа
 |
Рис. 1.50. Структурная схема дискретной системы
с коррекцией на входе непрерывной части
Дискретная система (см. рис. 1.49) характеризуется непрерывным сигналом ошибкии непрерывным выходным сигналом, поэтому при синтезе корректирующих устройств можно непосредственно применять методы непрерывных систем.






