Найдем решение однородного разностного уравнения в виде  , где z – некоторое число. Подставляя x(t) в разностное уравнение (2.1) при f(t)=0 и сокращая на zt, получаем характеристическое уравнение
, где z – некоторое число. Подставляя x(t) в разностное уравнение (2.1) при f(t)=0 и сокращая на zt, получаем характеристическое уравнение
 .
.
Если его корни z1, z2 вещественные и различные, то общее решение имеет вид
 .
.
Если z1 = z2, то в решении появляется линейный множитель
 .
.
В случае пары комплексно-сопряженных корней z1,2 = a±ib решение может быть записано в вещественной форме
 .
.
Здесь r – модуль комплексного числа z1, а j – его аргумент.
Формулы для уравнений более высоких порядков выглядят также, просто увеличивается число слагаемых в решении.
Пример 1. Решим разностное уравнение  .
.
Характеристическое уравнение имеет вид  .
.
Его корни вещественные и различные: z1 = 3, z2 = 2.
Общее решение:  .
.
Пример 2. Решим разностное уравнение  .
.
Характеристическое уравнение имеет вид  .
.
Его корни комплексные:  .
.
Их положение на комплексной плоскости z1,2 = a±ib показано на рис. 2.1.
Модуль и аргумент корней можно найти непосредственно на рис. 2.1:
r = 2, 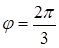 . Общее решение:
. Общее решение:  .
.
Произвольные постоянные сі находят, задавая начальные условия. Пусть, например, в примере 2 заданы начальные условия х(0) =2; х(1) =4. Записываем общее решение для t=0 и t=1:
 .
.

Рис. 2.1. Модуль и аргумент корней
Отсюда находим с2 = 2, с1 =  . Следовательно, решение имеет вид
. Следовательно, решение имеет вид  .
.
Общее решение неоднородного разностного уравнения представляет собой сумму общего решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения. Частное решение ищут в том же виде, что и правая часть, т.е. функция f(t) в уравнении (2.1):
– если f(t) – постоянная, то в виде константы;
– если f(t) – экспонента, то в виде экспоненты с тем же показателем;
– если f (t) =sin kt или cos kt, то в виде c1sinkt+c2coskt.
Коэффициенты с1 и с2 находят, подставляя частные решения в разностное уравнение и приравнивая одноименные функции справа и слева.
Пример 3. Дано неоднородное разностное уравнение второго порядка
 .
.
Находим корни характеристического полинома
 .
.
Частное решение ищем в виде хчаст=с. Подставляя его в исходное уравнение, находим, что хчаст=2.
Общее решение неоднородного уравнения получаем как сумму частного решения и общего решения соответствующего однородного уравнения
 .
.
Коэффициенты с1, с2 находим из уравнений 1=2+с2,  , откуда
, откуда  .
.
1.2. Решение разностных уравнений с помощью z -преобразования
При описании дискретных систем и решении разностных уравнений широко применяется аппарат z -преобразования – это дискретный аналог преобразования Лапласа. Например, умножение изображения F(p) на оператор Лапласа р соответствует дифференцированию непрерывной функции f(t). Умножение изображения F(z) на оператор z соответствует сдвигу функции f(t) (которая может быть непрерывной, дискретной или решетчатой) на один такт.
Таким образом, если операторы р и 1/р – это операторы дифференцирования и интегрирования, то операторы z и z-1 – это операторы сдвига влево и вправо. С инженерной точки зрения оператор z-1 представляет собой элемент задержки.
Существуют также определенные параллели между изображениями функций F(p) и F(z). Например, изображению по Лапласу F(p) = 1 соответствует дельта-функция f(t) = d(t), а изображению F(z) = 1, соответствует единичный импульс. В том и другом случае оригиналом является элементарное импульсное воздействие.
Краткая таблица z -преобразований других функций приведена на стр.22 (табл.1.2).
Пусть дано разностное уравнение n -го порядка
 (2.3)
(2.3)
с начальными условиями  .
.
Алгоритм его решения с помощью z -преобразования следующий:
– применим z -преобразование к уравнению (2.3), заменяя f(t) на F(z), y(t) на Y(z); y(t+ 1 ) на z(Y(z)-y0) и т.д.;
– из полученного алгебраического уравнения выразим Y(z);
– выполним разложение Y(z) на простые дроби;
– пользуясь табл.1.2 (стр.22), выполним обратное z -преобразование.
Результатом будет искомое решение разностного уравнения.
Пример 4. Требуется решить разностное уравнение второго порядка

с нулевыми начальными значениями y0, y1 и входным сигналом un = 1.
Решение:
– применяем к нему z -преобразование
 ;
;
– выражаем Y(z) и подставляем  :
:
 ;
;
– представляем правую часть в виде суммы простых дробей с переменной z в числителе:
 ,
,
разложение можно выполнить методом неопределенных коэффициентов или в пакете Matlab с помощью команды [R,P,K]=residue(B,А), где векторы В и А – коэффициенты полиномов числителя и знаменателя в порядке убывания степени z; синтаксис команды residue для Y(z) данного примера следующий: [R,P,K]=residue([1],[1 -6 11 -6]), в результате получим R – коэффициенты числителей суммы простых дробей, P – знаменатели простых дробей, K – свободный член;
– с помощью z -преобразований (табл.1.2, стр.22) или команды iztrans тулбокса SYMBOLIC пакета Matlab находим оригиналы каждого из слагаемых и суммируем их:  .
.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Задание и таблица вариантов
Дискретная система задана неоднородным разностным уравнением вида  . Для ее исследования необходимо решить заданное разностное уравнение с помощью характеристического полинома (см. п.1.1).
. Для ее исследования необходимо решить заданное разностное уравнение с помощью характеристического полинома (см. п.1.1).
Начальные условия: y0 = 0; y1 = 0.
Входной сигнал: un = 1.
Коэффициенты разностного уравнения a и b указаны в табл. 2.1.
Таблица вариантов 2.1
Коэффициенты a и b разностного уравнения 

Задание и таблица вариантов
Дискретная система задана неоднородным разностным уравнением вида  . Необходимо найти реакцию системы на входной сигнал un = 1, решив разностное уравнение, используя z -преобразование и последовательно рассчитав точки y2, …, y5 (см. п.1.2).
. Необходимо найти реакцию системы на входной сигнал un = 1, решив разностное уравнение, используя z -преобразование и последовательно рассчитав точки y2, …, y5 (см. п.1.2).
Начальные условия: y0 = 0; y1 = 0.
Коэффициенты разностного уравнения a и b указаны в табл. 2.2.
Таблица вариантов 2.2
Коэффициенты a и b разностного уравнения 
| № | ||||||||||
| b | -1.3 | -0.7 | -0.2 | -2 | -1.6 | 1.6 | -1.6 | 1.9 | -2.8 | 2.5 |
| a | 0.3 | -0.6 | -0.48 | 0.96 | 0.6 | 0.55 | 0.48 | 0.6 | 1.8 |
| № | ||||||||||
| b | 0.5 | -0.72 | -1.28 | -2 | 2.88 | -0.5 | -0.72 | -1.28 | -2 | -2.88 |
| a | -0.27 | -0.4 | -0.7 | -1.1 | 1.6 | -0.25 | -0.37 | -0.66 | -1.1 | 1.5 |
Привести числовое решение разностного уравнения, дискретную передаточную функцию, ее разложение на простые дроби и график yn.
Контрольные вопросы
Даны разностные уравнения:
1)  , ,
| 2)  , ,
|
3)  , ,
| 4)  , ,
|
5)  , ,
| 6)  , ,
|
7)  , ,
| 8)  , ,
|
9)  , ,
| 10) 
|
11)  , ,
| 12)  , ,
|
13) 
| 14) 
|
Требуется решить уравнение:
а) с помощью характеристического уравнения;
б) при помощи z -преобразования.
Лабораторная работа №3






