Одним з найефективнішим засобом забезпечення надійності в експлуатації і, як наслідок, якості машин є резервування заміщенням.
Для машин в експлуатації знаходять застосування такі показники надійності:
– середнє напрацювання на відмову 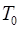 ;
;
– середній час відновлення працездатного стану 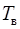 ;
;
– коефіцієнт готовності 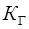 .
.
Перший показник надійності характеризує безвідмовність об’єкту і може бути визначений як відношення повної тривалості роботи об’єкта 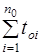 до повного числа зареєстрованих відмов
до повного числа зареєстрованих відмов 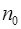
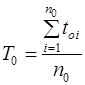 . (2.16)
. (2.16)
Другий показник характеризує ремонтопридатність об’єкта, його визначають як відношення сумарного часу, витраченого на відновлення 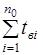 до загального числа відновлень, чисельно рівних кількості виниклих відмов
до загального числа відновлень, чисельно рівних кількості виниклих відмов 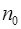 :
:
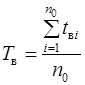 . (2.17)
. (2.17)
Коефіцієнт готовності 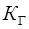 – комплексний показник надійності. Він кількісно характеризує властивості як безвідмовності об’єкта, так і ремонтопридатності, і визначається як ймовірність того, що об’єкт опиниться в працездатному стані в довільний момент часу:
– комплексний показник надійності. Він кількісно характеризує властивості як безвідмовності об’єкта, так і ремонтопридатності, і визначається як ймовірність того, що об’єкт опиниться в працездатному стані в довільний момент часу:
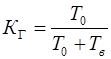 . (2.18)
. (2.18)
Можна вважати, що 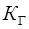 чисельно рівний частці працездатних об’єктів у будь-який момент часу.
чисельно рівний частці працездатних об’єктів у будь-який момент часу.
Для визначення перерахованих показників надійності ремонтованих об’єктів потрібний статистичний матеріал, який зазвичай збирається в умовах рядової експлуатації, або в умовах підконтрольних спеціальних випробувань.
Надійність об’єкту як системи, що складається з ряду елементів, можна визначити також по даним про надійність кожної її складової частини або елементу. Як правило, визначити показники надійності деталі або вузла простіше, ніж всієї системи в цілому. В даний час є необхідні методи і технічні засоби для випробування на надійність різних робочих органів, деталей, вузлів.
Надійність машини, як системи, залежить від її структури. Більшість машин і агрегатів – це системи з послідовною структурою, при якій відмова системи наступає у разі відмови будь-якого її елементу. Вид такої структури з трьох елементів представлений на рис. 2. 6. Це може бути, наприклад, ведучий міст базової машини, в якому елемент 1 – головна передача, елемент 2 – піввісь і елемент 3 – бортові редуктори. В цьому випадку говорять про послідовне з’єднання елементів в системі, а ймовірність безвідмовної роботи системи при незалежних відмовах елементів визначають по формулі:
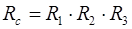 (2.19)
(2.19)
де 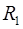 ,
, 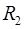 і
і 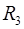 – ймовірність безвідмовної роботи елементів.
– ймовірність безвідмовної роботи елементів.
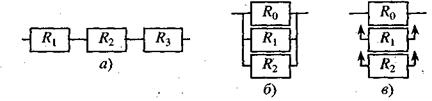
Рисунок 2.6 – Структурні схеми з трьох елементів:
а – послідовне з’єднання; б – паралельне з’єднання (постійне резервування);
в – резервування заміщенням
При недостатній надійності яких-небудь елементів надійність системи можна підвищити введенням надмірності, тобто шляхом резервування. Резервування буває постійним (навантаженим), структура якого приведена на рис. 2.6, б, або може здійснюватися шляхом заміщення (рис. 2.6, в). У останньому випадку маємо ненавантажений резерв, оскільки резервні елементи включаються в роботу тільки при відмові основного. Постійне резервування називають паралельним з’єднанням елементів. У разі незалежності відмов ймовірність безвідмовної роботи системи з паралельним з’єднанням трьох елементів (рис. 2.6, б) визначається за формулою
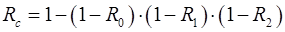 , (2.20)
, (2.20)
де 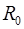 ,
, 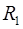 і
і 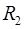 – ймовірність безвідмовної роботи основного і резервних елементів.
– ймовірність безвідмовної роботи основного і резервних елементів.
У мобільних машинах постійне резервування використовується значно рідше, ніж резервування заміщенням. При резервуванні заміщенням середнє напрацювання на відмову системи, що складається з одного основного (що працює) і К таких же резервних елементів, визначається за формулою
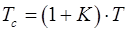 , (2.21)
, (2.21)
де 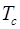 – середнє напрацювання на відмову елементу.
– середнє напрацювання на відмову елементу.
Середнє квадратичне відхилення 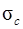 напрацювання на відмову цієї системи визначається з виразу
напрацювання на відмову цієї системи визначається з виразу
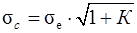 , (2.22)
, (2.22)
де 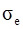 – середнє квадратичне відхилення напрацювання на відмову елементу.
– середнє квадратичне відхилення напрацювання на відмову елементу.
З (2.21) і (2.22) витікає, що коефіцієнти варіації напрацювання на відмову системи 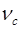 і елементу
і елементу 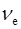 при резервуванні заміщенням зв’язані співвідношенням:
при резервуванні заміщенням зв’язані співвідношенням:
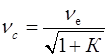 . (2.23)
. (2.23)
При розподілі напрацювання на відмову системи згідно із законом Вейбулла його параметр форми 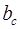 однозначно визначається величиною коефіцієнта варіації
однозначно визначається величиною коефіцієнта варіації 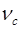 . Ця залежність при
. Ця залежність при 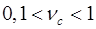 з достатньою для практичного використання точністю описується наближеним виразом:
з достатньою для практичного використання точністю описується наближеним виразом:
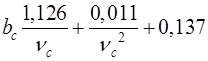 (2.24)
(2.24)
звідки, з обліком (2.23), витікає, що
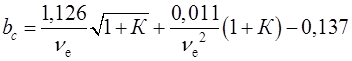 . (2.25)
. (2.25)
Параметр масштабу розподілу напрацювання на відмову системи, виходячи з (2.21) визначається по формулі:
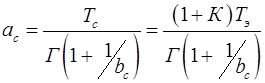 . (2.26)
. (2.26)
При зроблених припущеннях ймовірність безвідмовної роботи системи з того, що одного працює і К резервних (запасних) елементів, що послідовно включаються в роботу при настанні відмов на заданому інтервалі напрацювання 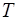 , визначається з виразу:
, визначається з виразу:
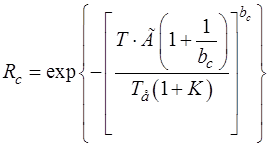 (2.27)
(2.27)
в якому параметр 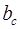 визначається за формулою (2.25).
визначається за формулою (2.25).
Ймовірність безвідмовної роботи елементу 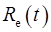 на інтервалі
на інтервалі 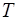 можна також визначати по формулі (2.27). Поклавши у ній
можна також визначати по формулі (2.27). Поклавши у ній 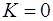 , отримаємо вираз:
, отримаємо вираз:
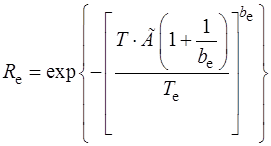 (2.28)
(2.28)
у якому параметр форми 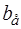 відповідно до (2.25) визначається за формулою
відповідно до (2.25) визначається за формулою
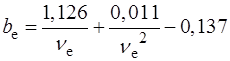 (2.29)
(2.29)
Величина 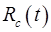 визначає ймовірність того, що за період
визначає ймовірність того, що за період 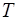 не наступить стан, при якому подальше відновлення працездатності системи стане вже неможливим через відсутність резервних елементів. Ймовірність того, що у будь-який момент часу система не знаходитиметься в стані відновлення за наявності резервних елементів, визначається величиною коефіцієнта готовності
не наступить стан, при якому подальше відновлення працездатності системи стане вже неможливим через відсутність резервних елементів. Ймовірність того, що у будь-який момент часу система не знаходитиметься в стані відновлення за наявності резервних елементів, визначається величиною коефіцієнта готовності 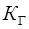 .
.
Ймовірність того, що ще не витрачені резервні елементи і система не знаходиться в стані відновлення, визначається твором вказаної вище ймовірності і є комплексним показником надійності резервованих способом заміщення систем, який називають коефіцієнтом оперативної готовності 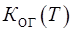 :
:
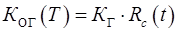 (2.30)
(2.30)
Величина цього показника відповідає заданому інтервалу часу роботи 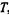 , із збільшенням якого коефіцієнт оперативної готовності монотонно зменшується. З його допомогою можна визначити середнє число працездатних машин до кінця періоду
, із збільшенням якого коефіцієнт оперативної готовності монотонно зменшується. З його допомогою можна визначити середнє число працездатних машин до кінця періоду 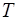 :
:
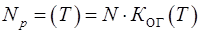 (2.31)
(2.31)
де – 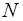 загальне число машин.
загальне число машин.
Bиконання завдання 2.3.
Таблиця 2.7 – Початкові дані до розрахунку коефіцієнта готовності
Напрацювання між відмовами 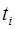
| 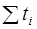 =15580 =15580
| ||||||||||
Час відновлення 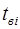
| 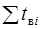 =485 =485
|
Відповідно до формул (2.16) (2.17) (2.20), середнє напрацювання на відмову системи:
T0= 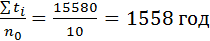
середній час відновлення
Тв= 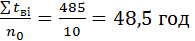
коефіцієнт готовності
Кг= 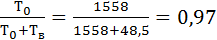 .
.
Таблиця 2.11 – Початкові дані і результати розрахунку ймовірності безвідмовної роботи елементів
| № елементу | 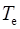 , год , год
| 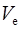 , год , год
| 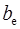
| 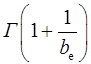
| Re(1000) |
| 0,6 | 1,77 | 0,9406 | 0,88 | ||
| 0,4 | 2,75 | 0,9131 | 0,89 | ||
| 0,7 | 1,49 | 0,9525 | 0,88 |
Ймовірність безвідмовної роботи нерезервованої системи
Rис(1000)=0,88.0,89.0,88=0,69.
Таблиця 2.12.Результати розрахунку ймовірності безвідмовної роботи за варіантами заміщення згідно рисунку 2.7
| Варіанти заміщення згідно рисунку 2.7 | |||||
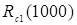
| 0,99 | 1,0 | 0,99 | 0,99 | 1,0 |
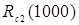
| 1,0 | 0,99 | 0,99 | 0,89 | 0,89 |
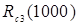
| 0,88 | 0,88 | 0,99 | 1,0 | 0,99 |
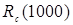
| 0,87 | 0,87 | 0,97 | 0,88 | 0,88 |
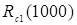
| 0,88 | 0,88 | 1,0 | 0,88 | 0,88 |
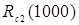
| 0,99 | 1,0 | 0,89 | 0,89 | 1,0 |
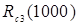
| 1,0 | 0,99 | 0,88 | 1,0 | 0,88 |
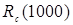
| 0,87 | 0,87 | 0,78 | 0,78 | 0,77 |
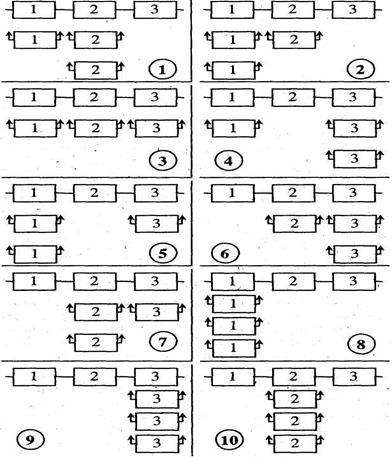
Рисунок 2.7 – Варіанти резервування елементів в системі
Ймовірність безвідмовної роботи за варіантом 1:
Rc1(1000)=1-(1-Re1)2=1-(1-0,88)2=0,99;
Rc2(1000)=1-(1-Re2)3=1-(1-0,89)3=1;
Rc3(1000)=Re3=0,88;
Rc(1000)=Rc1.Rc2.Rc3=0,99.1,0.0,88=0,87
Ймовірність безвідмовної роботи за варіантом 2:
Rc1(1000)=1-(1-Re1)3=1-(1-0,88)3=1,0;
Rc2(1000)=1-(1-Re2)2=1-(1-0,89)2=0,99;
Rc3(1000)=Re3=0,88;
Rc(1000)=Rc1.Rc2.Rc3=1,0.0,99.0,88=0,87.
Ймовірність безвідмовної роботи за варіантом 3:
Rc1(1000)=1-(1-Re1)2=1-(1-0,88)2=0,99;
Rc2(1000)=1-(1-Re2)2=1-(1-0,89)2=0,99;
Rc3(1000)=1-(1-Re3)2=1-(1-0,88)2=0,99;
Rc(1000)=Rc1.Rc2.Rc3=0,99.0,99.0,99=0,97.
Ймовірність безвідмовної роботи за варіантом 4:
Rc1(1000)=1-(1-Re1)2=1-(1-0,88)2=0,99;
Rc2(1000)=Re2=0,89;
Rc3(1000)=1-(1-Re3)3=1-(1-0,88)3=1,0;
Rc(1000)=Rc1.Rc2.Rc3=0,99.0,89.1,0=0,88.
Ймовірність безвідмовної роботи за варіантом 5:
Rc1(1000)=1-(1-Re1)3=1-(1-0,88)3=1,0;
Rc2(1000)=Re2=0,89;
Rc3(1000)=1-(1-Re3)2=1-(1-0,88)2=0,99;
Rc(1000)=Rc1.Rc2.Rc3=1,0.0,89.0,99=0,88.
Ймовірність безвідмовної роботи за варіантом 6:
Rc1(1000)=Re1=0,88;
Rc2(1000)=1-(1-Re2)2=1-(1-0,89)2=0,99;
Rc3(1000)=1-(1-Re3)3=1-(1-0,88)3=1,0;
Rc(1000)=Rc1.Rc2.Rc3=0,88.0,99.1,0=0,87.
Ймовірність безвідмовної роботи за варіантом 7:
Rc1(1000)=Re1=0,88;
Rc2(1000)=1-(1-Re2)3=1-(1-0,89)3=1,0;
Rc3(1000)=1-(1-Re3)2=1-(1-0,88)2=0,99;
Rc(1000)=Rc1.Rc2.Rc3=0,88.1,0.0,99=0,87.
Ймовірність безвідмовної роботи за варіантом 8:
Rc1(1000)=1-(1-Re1)4=1-(1-0,88)4=1,0;
Rc2(1000)=Re2=0,89;
Rc3(1000)=Re3=0,88;
Rc(1000)=Rc1.Rc2.Rc3=1,0.0,89.0,88=0,78.
Ймовірність безвідмовної роботи за варіантом 9:
Rc1(1000)=Re1=0,88;
Rc2(1000)=Re2=0,89;
Rc3(1000)=1-(1-Re3)4=1-(1-0,88)4=1,0;
Rc(1000)=Rc1.Rc2.Rc3=0,88.0,89.1,0=0,78.
Ймовірність безвідмовної роботи за варіантом 10:
Rc1(1000)=Re1=0,88;
Rc2(1000)=1-(1-Re2)4=1-(1-0,89)4=1,0;
Rc3(1000)=Re3=0,88;
Rc(1000)=Rc1.Rc2.Rc3=0,88.1,0.0,88=0,78.
Для варіанта 3, у якого 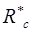 вище, розраховуємо ймовірність безвідмовної роботи при резервуванні заміщенням при К=1.
вище, розраховуємо ймовірність безвідмовної роботи при резервуванні заміщенням при К=1.
Rc1(1000)= 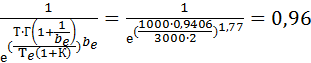
Rc2(1000)= 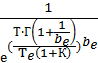 =
= 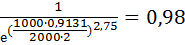
Rc3(1000)= 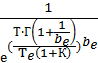 =
= 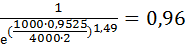
Rc= Rc1(1000). Rc2(1000). Rc3(1000)=0,96.0,98.0,96=0,90
Коефіцієнт оперативної готовності
Kог=Кг.Rc(t)=0,97.0,90=0,873.
Величини 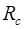 і
і 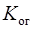 при значеннях T=1500 год. і Т=2000 год. розраховуємо аналогічно і заносимо в табл. 2.13.
при значеннях T=1500 год. і Т=2000 год. розраховуємо аналогічно і заносимо в табл. 2.13.
Таблиця 2.13 – Результати розрахунків 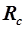 і
і 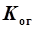
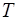
| ||||
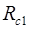
| 0,96 | 0,93 | 0,88 | |
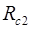
| 0,98 | 0,95 | 0,89 | |
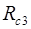
| 0,96 | 0,93 | 0,88 | |
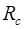
| 0,90 | 0,82 | 0,69 | |
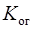
| 0,97 | 0,873 | 0,795 | 0,669 |
Будуємо графіки 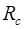 і
і 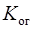 у функції Т і визначуваний період роботи, відповідний заданому значенню:
у функції Т і визначуваний період роботи, відповідний заданому значенню: 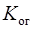 =0,9
=0,9






