Прогнозування показників якості

 

Довговічність є одним з найважливіших показників якості. Довговічність – це властивість об’єкта зберігати працездатність до настання граничного стану при встановленій системі технічного обслуговування і ремонту. При цьому, під граничним станом розуміють такий стан об’єкта, при якому його подальше застосування за призначенням неприпустиме або недоцільне, або відновлення його справного або працездатного стану неможливе або недоцільне. Довговічність оцінюється ресурсом, тобто напрацю­ванням до граничного стану.

Для деталей, що зношуються, вважається, що граничний стан визначається граничним розміром деталі. Зазвичай вдається зміряти знос 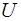через відомі проміжки часу і побудувати реалізації зносу у вигляді функції

,

 

де і параметри закону.

Параметр може змінютися в широких межах, а параметр для виробу одного найменування змінюється трохи і задається заздалегідь. Прийнята функція використовується для розрахунку і прогнозування довговічності досліджуваного об’єкта.

Припустимо, є п вимірювань зносу об’єктів одного найме­ну­вання, наприклад, пальців гусеничного ланцюга базової машини через певний проміжок часу . Для кожного об’єкта справедлива залежність

 

. (2.10)

 

Тоді величина 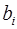для і -го об’єкта знаходиться за наявним вимірюванням :

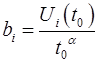. (2.11)

Можна припустити, що середнє значення зносу U і середнє квадратичне відхилення у вибірці з 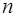об’єктів змінюються в часі за таким же статечним законом (рис. 2.3):

 

(2.12)

 

(2.13)

 

 

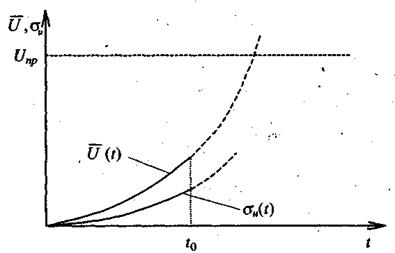
Рисунок 2.3 – Зміна середнього значення зносу і середнього квадратичного відхилення залежно від напрацювання t

 

Параметри 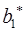і визначаються за значеннями і

у момент вимірювання (через час роботи об’єкта )

 

; . (2.14)

 

 

Підставивши (3.2) в (3.1), отримаємо

 

; . (2.15)

Середнє значення і середнє квадратичне відхилення зносу змінюються в часі, а відмова наступає при досягненні кожним об’єктом граничного значення зносу. Для випадку, якщо знос розподілений за нормальним законом, ймовірність безвідмовної роботи визначається за формулою

 

, (2.16)

 

де 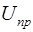– гранично допустимий знос об’єкта;

– табульована функція Лапласа.

Для заданих значень будується графік ймовірності безвідмовної роботи і визначається гамма-відсодковий ресурс.

Виконання завдання 2.2. Початкові дані для розрахунків отримують вимірюванням мінімального поперечного розміру пальців гусеничного ланцюга базової машини, що пропрацювала час . Вимірювання проводять в шести перетинах (рис. 2.4) трьох пальців, що працюють в парі з проушиной ланки і що мають явно виражені сліди зносу.

 

 

Рисунок 2.4 – Схема розташування поперечних перетинів для вимірювання зносу пальця гусеничного ланцюга

 

Результати вимірювань вносимо до табл. 2.4.

Обчислення зручно вести в табл. 2.5 і 2.6. Значення і задаються. Граничне значення зносу для пальців гусеничного ланцюга і початковий діаметр пальця прийняти ; відповідно.

Робота закінчується побудовою графіка ймовірності безвідмовної роботи пальців ланцюга (рис. 2.5) і визначенням 80-відсоткового ресурсу.

 

Результати вимірювань мінімального поперечного розміру пальців в різних перетинах, після напрацювання = 1000 год, наведені в табл. 2.4.

Таблиця 2.4 – Результати вимірювань розмірів поперечних перетинів пальців , мм

Номер пальця	Номер перетину
I-I	II-II	III-III	IV-IV	V-V	VI-VI
	20,0	19,8	20,5	18,9	19,8	20,2
	19,6	18,5	20,0	18,6	18,7	18,6
	20,5	19,3	18,7	18,9	20,3	18,8

 

Таблиця 2.5 – Результати розрахунків

 

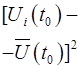
i			i
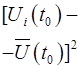
	2,0	0,32		3,4	0,69
	2,2	0,14		3,3	0,53
	1,5	1,14		3,4	0,69
	3,1	0,28		1,5	1,14
	2,2	0,14		2,7	0,02
	1,8	0,59		3.3	0,53
	2,4	0,03	16	3,1	0,28
	3,5	0,86		1,7	0,76
	2,0	0,32		3,2	0,40
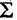
				46,3 мм	8,86

 

Відповідно до (2.14)

 

мм;

 

Коефіцієнти 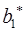; (2.15) рівні відповідно:

 

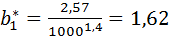^.10^-4

^.10^-4

 

Таблиця 2.6 – Результати обчислення ймовірності безвідмовної роботи пальців ланцюга

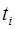
	31,45	9,66	3,97	1,47	0,12	–0,71	–1,27
	1,0	1,0	1,0	0,929	0,548	0,239	0,102

 

За отриманими даними побудований графік ймовірності безвідмовної роботи пальців ланцюга (рис. 4.3), на якому представлений 80 %-й ресурс 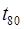=1 750 год.Обчисленнянаведені в табл. 2.6, виконані для .

 

 

Рисунок 2.5 – Графік ймовірності безвідмовної роботи
пальців гусеничного ланцюга