Практично у всіх випадках надійність машини є основним показником її якості. Для машин знаходять застосування такі показники надійності [2]:
середнє напрацювання на відмову, T;
ймовірність безвідмовної роботи,  ;
;
гамма-відсотковий ресурс,  .
.
Для визначення показників надійності необхідний статистичний матеріал про відмови в експлуатації машин.
Відомо, що закон розподілу ресурсу t добре описується універсальним двохпараметричним законом Вейбулла-Гнеденко, для якого функція розподілу має вигляд
 , (2.1)
, (2.1)
де  і
і  – параметри закону.
– параметри закону.
Невідомі параметри,  і
і  можуть бути визначені аналітично або графічно.
можуть бути визначені аналітично або графічно.
Параметри  і
і  пов’язані з середнім напрацюванням на відмову T, середнім квадратичним відхиленням
пов’язані з середнім напрацюванням на відмову T, середнім квадратичним відхиленням  і коефіцієнтом варіації
і коефіцієнтом варіації  залежностями
залежностями
 ;(2.2)
;(2.2)
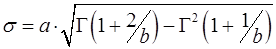 ; (2.3)
; (2.3)
 . (2.4)
. (2.4)
В формулах (2.3) і (2.4)  – гамма-функція, що визначається за таблицями [2].
– гамма-функція, що визначається за таблицями [2].
Ймовірність безвідмовної роботи  в інтервалі від 0 до t
в інтервалі від 0 до t
 , (2.5)
, (2.5)
де F (t)– функція розподілу ресурсу, визначувана у разі закону Вейбулла-Гнеденко співвідношенням (2.1).
Гамма-відсотковий ресурс знаходять графічно.
Довірчі межі для середнього напрацювання на відмову Т і ймовірність безвідмовної роботи  обчислюють із співвідношень
обчислюють із співвідношень
 (2.6)
(2.6)
 , (2.7)
, (2.7)
де  – квантиль нормального розподілу, що відповідає ймовірності.
– квантиль нормального розподілу, що відповідає ймовірності.
Довірчі межі для гамма-відсоткового ресурсу визначають графічно.
При повних випробуваннях всі об’єкти доводяться на відмову, і результатом випробувань є вибірка напрацювань на відмову – 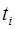 , i= 1, 2. .., N.
, i= 1, 2. .., N.
Для знаходження апроксимуючого закону розподілу напрацювання на відмову необхідне знання емпіричної функції розподілу  .
.
З цією метою:
Весь діапазон значень випадкової величини 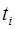 розбивають на K інтервалів однакової довжини h. Далі визначають значення відносної частоти (частості)
розбивають на K інтервалів однакової довжини h. Далі визначають значення відносної частоти (частості) 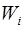 попадання напрацювань в і -й інтервал
попадання напрацювань в і -й інтервал
 , (2.8)
, (2.8)
а потім емпіричну функцію розподілу 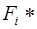 :
:
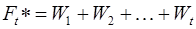 (2.9)
(2.9)
при цьому в кінці останнього k -го інтервала  = 1.
= 1.
При графічному вписуванні теоретичного закону Вейбулла-Гнеденко і визначенні його параметрів  і
і  на спеціальному імовірнісному папері по осі абсцис відкладають значення правих меж інтервалу
на спеціальному імовірнісному папері по осі абсцис відкладають значення правих меж інтервалу  , а по осі ординат – відповідні даному інтервалу значення емпіричної функції розподілу
, а по осі ординат – відповідні даному інтервалу значення емпіричної функції розподілу 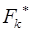 , в результаті отримують точки, через які проводять пряму так, щоб вона проходила за можливість ближче до всіх точок. Побудована пряма є графіком теоретичного розподілу
, в результаті отримують точки, через які проводять пряму так, щоб вона проходила за можливість ближче до всіх точок. Побудована пряма є графіком теоретичного розподілу 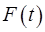 .
.
Шукані параметри а і  теоретичного закону визначають (рис. 2.1) таким чином:
теоретичного закону визначають (рис. 2.1) таким чином:
 – безпосередньо з графіка;
– безпосередньо з графіка;

де  – кут нахилу прямої до осі абсцис.
– кут нахилу прямої до осі абсцис.
Після визначення середнього напрацювання на відмову Т і значень ймовірності  за формулами (2.1) і (2.6) відповідно, проводять розрахунок цих же величин з довірчими межами, використовуючи залежності (2.6) і (2.7), і будують графік
за формулами (2.1) і (2.6) відповідно, проводять розрахунок цих же величин з довірчими межами, використовуючи залежності (2.6) і (2.7), і будують графік  (рис. 2.2).
(рис. 2.2).
Гамма-відсотковий ресурс  знаходять графічно.
знаходять графічно.
Виконання завдання 2.1.
За наслідками повних випробувань на відмову 50 машин побудувати графік ймовірності безвідмовної роботи  , знайти середній Т і 80 %-й ресурси з довірчими межами (
, знайти середній Т і 80 %-й ресурси з довірчими межами (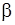 =90 % і
=90 % і  = 1,645) при початкових даних, відповідних напрацюванням до відмов:
= 1,645) при початкових даних, відповідних напрацюванням до відмов:
190; 320; 300; 260; 540; 180; 980; 580; 740; 260; 1150; 830; 930; 370; 510; 150; 660; 190; 420; 1350; 350; 570; 490; 1080; 250; 1540; 340; 550; 930; 370; 626; 624; 622; 495; 916; 619; 496; 600; 1059; 997; 285; 416; 349; 1014; 663; 652; 639; 788; 461; 708.
З приведеного ряду значень знаходимо мінімальне  =150 год і максимальне
=150 год і максимальне  =1540 год.
=1540 год.
Розмах вибірки
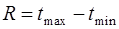 = 1540-150 = 1390.
= 1540-150 = 1390.
Приймаємо число інтервалів  . Довжина інтервалу
. Довжина інтервалу
 =
=  =173,75 год, приймаємо
=173,75 год, приймаємо  =200 год. Результати подальших обчислень наведені в табл. 2.1, за матеріалами якої побудований графік (рис. 2.1) і розраховані:
=200 год. Результати подальших обчислень наведені в табл. 2.1, за матеріалами якої побудований графік (рис. 2.1) і розраховані:
– параметри закону розподілу Вейбулла-Гнеденко
 =700 год;
=700 год;  =1,3
=1,3  .1,67=2,171.
.1,67=2,171.
– середній ресурс з довірчими межами при 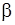 = 0,9;
= 0,9;  =1,65;
=1,65;
T= 700.Г(1+  649,5; σ =700
649,5; σ =700  233,8;
233,8;
 год;
год;
Тmax=703,8 год; Тmin=595,2 год.
80 %-й ресурс з довірчими межами (за графіком)
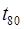 =350 год;
=350 год; 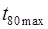 =450 год;
=450 год;  =260 год.
=260 год.
Таблиця 2.1 - Результати розрахунків за варіантом
| № | Межі інтервалів
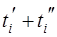
| Число відмов машин в інтервалі

| Частість
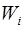
| Емпіріч. функція
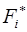
| Теоретич. функція

| Ймовірність. безвідм. роботи

| Довірчий інтервал

|
| 0-200 | 0,08 | 0,08 | 0,0639 | 0,9361 | 0,8790-0,9932 | ||
| 200-400 | 0,22 | 0,30 | 0,2569 | 0,7431 | 0,6411-0,8451 | ||
| 400-600 | 0,24 | 0,54 | 0,5113 | 0,4887 | 0,3721-0,6053 | ||
| 600-800 | 0,22 | 0,76 | 0,7374 | 0,2626 | 0,1599-0,3653 | ||
| 800-1000 | 0,12 | 0,88 | 0,8859 | 0,1141 | 0,0399-0,1883 | ||
| 1000-1200 | 0,08 | 0,96 | 0,96023 | 0,0,977 | 0-0,08537 | ||
| 1220-1400 | 0,02 | 0,98 | 0,98896 | 0,01104 | 0-0,03542. | ||
| 1400-1600 | 0,02 | 1,00 | 0,997574 | 0,002426 | 0-0,01391 | ||
| å | 1,00 |
За отриманими даними побудований (рис. 2.2) графік ймовірності безвідмовної роботи машин, на якому показані довірчі межі  , 80%-й ресурс
, 80%-й ресурс  і його довірчі межі.
і його довірчі межі.






