Припустимо, що в розглянутій задачі про якість різних (m) партій вироби виготовлялися на різних (l) верстатах і потрібно з'ясувати, чи є суттєві відмінності в якості виробів по кожному фактору: А - партія виробів, В - верстат. В результаті ми приходимо до задачі двофакторного дисперсійного аналізу.
Усі наявні дані представимо у вигляді табл. 5.4, в якій по рядках - рівні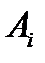 
фактора А, по стовпцях - рівні 
чинника В, а у відповідних комірчинах таблиці знаходяться значення показника якості виробів 
Двофакторна дисперсійна модель має вигляд:
, (5.14)
де 
- значення спостереження в осередку ij з номером k;
- загальна середня;
- ефект, обумовлений впливом i -го рівня фактора А;
- ефект, обумовлений впливом j -го рівня фактора В;
- ефект, обумовлений взаємодією двох факторів, тобто відхилення від середнього за спостереженнями у клітинці ij від суми перших трьох доданків в моделі (5.14);
- збурення, обумовлене варіацією змінної в середині окремої комірки.
Таблиця 5.4
| В А |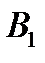 
| 
| … | 
| … | 
|
| 
| 
| … | 
| … | 
|
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
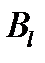
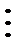
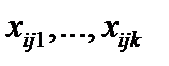
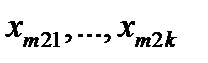
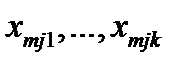
Вважаємо, що має нормальний закон розподілу 
, а всі математичні сподівання 
дорівнюють нулю. Групові середні знаходяться за формулами:
по клітинці – 
(5.15)
по рядку – 
(5.16)
по стовпцю – 
(5.17)
Загальне середнє - 
(5.18)
Таблиця 5.5 – таблиця дисперсійного аналізу.
Можна показати, що перевірка нульових гіпотез 
про відсутність впливу на розглянуту змінну факторів А, В та їх взаємодії АВ здійснюється порівнянням відношень 
(для моделі I з фіксованими рівнями факторів) або відношень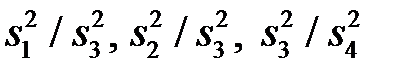 
(для випадкової моделі ІІ) з відповідними табличними значеннями F - критерію Фішера-Снедекора. Для змішаної моделі III перевірка гіпотез щодо факторів із фіксованими рівнями проводиться так само, як у моделі II, а факторів із випадковими рівнями - як в моделі I.
Якщо n = 1, тобто при одному спостереженні в осередку, то не всі нульові гіпотези можуть бути перевірені, оскільки випадає компонента 
із загальної суми квадратів відхилень, а з нею і середній квадрат 
, бо в цьому випадку не може бути мови про взаємодію чинників.
Таблиця 5.5
| Компоненти дисперсії | Сума квадратів | Число степенів вільності | Середні квадрати |
| Міжгрупова (фактор А) | 
| m -1 | 
|
| Міжгрупова (фактор В) | 
| l- 1 | 
|
| Взаємодія (АВ) |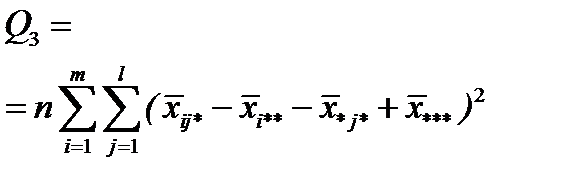 
| (m -1)(l -1) | 
|
| Залишкова | 
| mln-ml | 
|
| Загальна | 
| mln -1 |
◄ Приклад 5.2. У табл. 5.6 наведені добові прирости (г) відібраних для дослідження 18 поросят в залежності від методу утримання поросят (фактор А) та якості їх годівлі (фактор В). Необхідно на рівні значущості
= 0,05 оцінити суттєвість (достовірність) впливу кожного фактора і їх взаємодії на добовий приріст ваги поросят.
Розв’язання. Маємо m = 3, l = 2, n = 3. Визначимо (в г) середні значення приросту ваги:
в осередках – за (5.15): 
;
і аналогічно,
Таблиця 5.6
| Кількість голів в групі (фактор А) | Вміст протеїну в кормі, г (фактор В) | |
| Кількість голів в групі (фактор А) | В1=80 | В2=100 |
| А1 = 30 | 530, 540, 550 | 600, 620, 580 |
| А2 = 100 | 490, 510, 520 | 550, 540, 560 |
| А3 = 300 | 430, 420, 450 | 470, 460, 430 |
; 
по рядках – за (5.16): 
і, аналогічно
по стовпцях - за (5.17): 
і, аналогічно 
Загальний середній приріст - за (5.18):
Всі середні значення приросту (г) відобразимо у табл. 5.7. З таблиці 5.7 випливає, що зі збільшенням кількості голів у групі середній добовий приріст поросят у середньому зменшується, а при збільшенні вмісту протеїну в кормі - в середньому збільшується. Але чи є ця тенденція достовірною або пояснюється випадковими причинами? Для відповіді на це питання за формулами табл. 5.5 обчислимо необхідні суми квадратів відхилень:
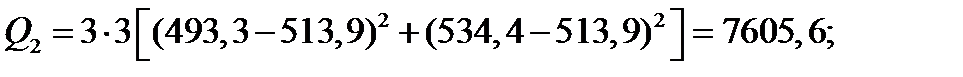
Середні квадрати знаходимо діленням отриманих сум на відповідну їм кількість степенів вільності m- 1= 2, l -1 = 1; (m -1) (l -1) = 2; mln - ml = 18-6 = 12; mln- 1 = 18-1 = 17.
Таблиця 5.7
| Кількість голів у групі (фактор А) | Вміст протеїну в кормі, г (фактор В) | ||
| 
| 
| |
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
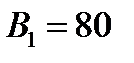
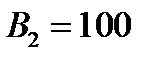
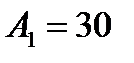
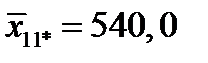
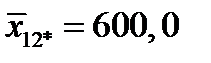
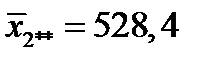
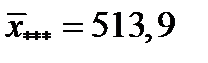
Результати зведемо в табл. 5.8.
Очевидно, дані фактори мають фіксовані рівні, тобто ми знаходимося в рамках моделі I. Тому для перевірки істотності впливу факторів А, В та їх взаємодії АВ необхідно знайти відношення:
і порівняти їх з табличними значеннями відповідно 
.
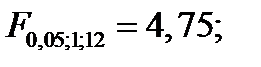
Таблиця 5.8
| Компонента дисперсії | Суми квадратів | Число степенів вільності | Середні квадрати |
| Міжгрупова (фактор А) Міжгрупова (фактор В) Взаємодія (АВ) |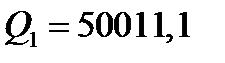 
| 
| |
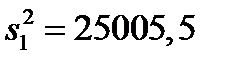
| Залишкова | 
| 
| |
| Загальна |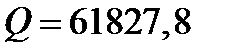 
|
Оскільки 
і 
, то вплив методу утримання поросят (фактору А) та якості їх годівлі (фактора В) є істотним. В силу того що 
, взаємодія зазначених факторів незначна. ►
Зауваження. З точки зору техніки обчислень для знаходження сум квадратів 
доцільніше використовувати формули:
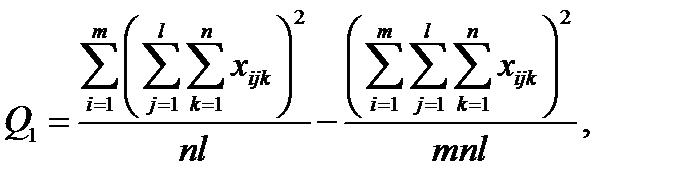(5.19)
(5.20)
(5.21)
(5.22)
. (5.23)
Так, у розглянутому прикладі 5.2:
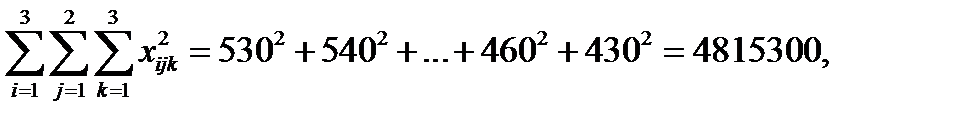
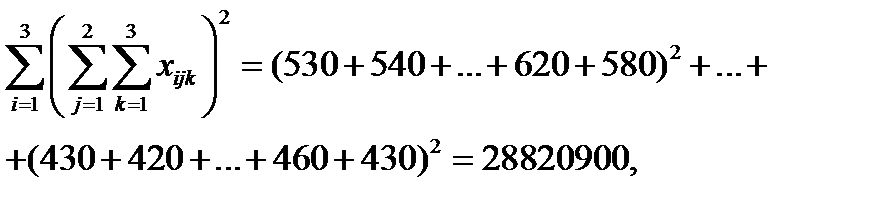
і за формулами (5.19) - (5.23):
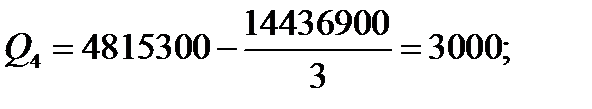
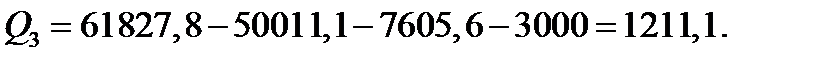
При вирішенні реальних завдань методом дисперсійного аналізу використовуються статистичні програмні пакети.
Відхилення від основних передумов дисперсійного аналізу - нормальності розподілу досліджуваної змінної і рівності дисперсій в осередках (якщо воно не надмірне) - не позначається істотно на результатах при рівному числі спостережень в осередках, але може бути дуже чутливим при нерівному їх числі. Крім того, при нерівному числі спостережень в осередках різко зростає складність апарату дисперсійного аналізу. Тому рекомендується планувати схему з рівним числом спостережень в осередках, а якщо зустрічаються відсутні дані, то відшкодовувати їх середніми значеннями інших спостережень в осередках. При цьому, проте, штучно введені відсутні дані не слід враховувати при обчисленні степенів вільності.
Контрольні питання
1. В чому полягає сутність дисперсійного аналізу?
2. За яких умов застосовують однофакторний дисперсійний аналіз?
3. За яких умов застосовують двофакторний дисперсійний аналіз?
4. Як інтерпретувати результати дисперсійного аналізу?
РОЗДІЛ 6
