Для сучасного підходу до оптимізації характерна формалізація задачі. Задача формулюється стандартним чином, після чого подальший її розв’язок проводиться на основі чіткого однозначного рецепту – алгоритму.
Формалізація, по-перше, дозволяє однозначно вирішувати самі різносторонні задачі. По-друге, формалізовані задачі пристосовані для вирішення на ЕОМ. Застосування обчислювальної техніки забезпечує можливість розгляду великого числа варіантів і вибору з них оптимального. Тому формалізація приводить до різкого підвищення ефективності процедури розв’язку задачі.
При формалізації задачі оптимізації виникає важливе діалектичне протиріччя. Задача розпадається на три основні етапи: 1) формулювання задачі, приведення її до однієї з стандартних форм; 2) знаходження оптимальних умов на основі алгоритму оптимізації; 3) реалізація оптимальних умов на практиці. Методи розв’язку на першому і другому етапах є взаємно протилежними: другий етап, як правило, в цілому формалізований на основі алгоритму розв’язку, а перший етап - не формальний. Тут не допоможе математика. Перший етап розв’язку задачі пов’язує конкретні особливості об’єкту з загальним методом розв’язку.
Якщо задача оптимізації погано сформульована, то правильний її розв’язок дає абсурдний результат на практиці. Інколи саме правильне формулювання задачі визначає успіх оптимізації в цілому.
Деякі проблеми, що виникають при формулюванні задач оптимізації, проілюструємо на прикладах.
Приклад 1. Проблеми формулювання задач оптимізації.
1. Припустимо, що ми розглядаємо процес розкладу апатиту сульфатною кислотою з отриманням фосфатної кислоти:
Ca5(PO4)3F+5H2SO4+5nH2O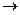 
3H3PO4+HF+5CaSO4.nH2O.
Задачу щодо оптимізації реактора розкладу (екстрактора) сформулюємо таким чином: створити апаратуру і вибрати такий режим, щоб ступінь розкладу апатиту був найбільшим, концентрація отриманої фосфатної кислоти – також найбільшою, а витрати – найменшими. Нижче ми побачимо, що в такій постановці задача, як правило, не розв’язується; але припустимо, що все ж нам вдається її розв’язати. Тоді виявиться, що знайдений оптимальний результат не реалізується на практиці.
Ми не врахували того, що у виробництві фосфатної кислоти одна з найскладніших операцій – це відокремлення кальцій сульфату від фосфатної кислоти. Тому ключовим моментом в формулюванні даної задачі є забезпечення таких умов кристалізації СаSO4, за яких отримуються кристали, які добре відокремлюються від розчину.
Таким чином, на етапі формулювання задачі необхідно враховувати фізико-хімічні особливості процесу, його економічність, загальну тенденцію в розвитку промисловості та багато інших обставин.
Як правило, формулювання задачі оптимізації включає вибір критерію оптимізації, встановлення обмежень, вибір оптимізуючих факторів та запис цільової функції.
Критерій оптимізації - це головна ознака, яка визначає наскільки добре функціонує дана система, реалізується даний процес, наскільки добре вирішена задача оптимізації.
Про роботу судять за її результатами. Тому критерій оптимізації є одним з головних результатів, одним з виходів системи. Щоб обраний критерій оптимізації можна було ефективно використовувати на наступному етапі, він повинен задовольняти такі три основні вимоги.
Перша вимога: критерій оптимізації повинен бути єдиним. Це сама важлива і складна вимога. Справа в тому, що, як правило, нас цікавить ряд виходів системи, і ми хочемо, щоб за всіма виходами система була найкращою.
Приклад 2. Співставлення двох критеріїв оптимізації.
Оптимізується робота ректифікаційної колони; бажано отримати максимально чисті продукти (тобто забезпечити найбільшу якість розділення). Але, якщо прагнути тільки до покращення цього показника, то „оптимальним” виявиться режим при безкінечному флегмовому числі, тобто без живлення і без відбору дистиляту. Продуктивність в такому „оптимумі” дорівнює нулю.
З іншої сторони, якщо ми будемо намагатись лише збільшити продуктивність, то прийдемо до протилежного (але також абсурдного) рішення: використовуючи колону просто як трубопровід, ми зможемо пропустити через неї величезну кількість суміші, але розділення виявиться нульовим.
В подальшому стане зрозуміло, що можна користуватись або одним, або іншим критерієм (ввівши обмеження). Але обома зазначеними критеріями одночасно користуватись неможливо: вони висувають до технологічного режиму несумісні вимоги.
В наш час запроваджується ряд спроб розробити процедуру оптимізації за декількома критеріями, але зазначеної методики (придатної для широкого використання) поки що немає. Ми вміємо оптимізувати лише за одним критерієм.
Тому так важливо добре вибрати критерій оптимізації. Складність такого вибору частково відображена в зазначених прикладах 1 і 2. Саме невдало вибраний критерій може зробити всю задачу безглуздою.
Як правило, найбільш обґрунтовані і найбільш добре працюють економічні критерії – такі, як прибуток, норма прибутку, рентабельність, приведений дохід, собівартість. Але характер залежності цих критеріїв від вхідних параметрів системи є складним. Для спрощення задачі часто користуються такими технологічними критеріями – продуктивністю, чистотою продукту, виходом продукту тощо. Кожний технологічний критерій в кінцевому рахунку пов'язаний з економікою, а саме: чим більша продуктивність, тим вищим буде прибуток; чим вища чистота продукту, тим менші будуть витрати на наступних стадіях тощо.
При оптимізації виробництва в цілому чи його окремих підрозділів застосовують економічні критерії. Технологічні критерії зручні при оптимізації дрібніших об’єктів - окремих вузла, апарату, невеликого ланцюжка апаратів, тобто при локальній оптимізації. При їх застосуванні необхідно особливо ретельно враховувати особливості процесу, а саме: критерій, який придатний в одних умовах, може абсолютно не підходити для інших умов.
Приклад 3. Критерії при оптимізації хімічної реакції.
Якщо відбувається єдина реакція типу:
Реагенти 
Продукти,
тобто реакція, в якій відсутні побічні стадії, то за критерій оптимальності, зазвичай, можна прийняти швидкість реакції v. Дійсно, чим вища v, тим при заданому ступені перетворення х, меншим виявиться необхідний розмір апарата Vа, або при даному Vа тим більшим буде х. Єдина реакція відбувається оптимально тоді, коли в кожній точці апарата вона реалізується з найбільш можливою швидкістю.
Але якщо є побічні стадії, то v, зазвичай, не підходить як критерій оптимізації. Дійсно, прискорення цільової реакції може відбуватись за таких умов, коли побічні стадії при цьому прискорюються ще більше. Прискорюючи швидкість цільової стадії реакції, ми отримаємо низьку селективність. В цьому випадку необхідно користуватись більш складними критеріями:
(79)
де F – критерій; gj – кількість речовини J на виході; n – загальна кількість речовин; mj і mV – коефіцієнти, що визначають надлишок (чи витрату), отриманий від одиниці речовини, і витрату на одиницю об’єму апарата.
Таким чином, критерій (79) має економічний характер, але він виражений через технологічні параметри.
Друга вимога: критерій оптимізації повинен виражатись числовим значенням. Інакше співставлення різних варіантів пов’язане з великими труднощами.
Приклад 4. Оптимізація за критерієм краси.
Завод розробив ряд зразків сувенірів. Для впровадження з них необхідно вибрати п’ять кращих. Очевидно, критерієм вибору буде краса, привабливість сувенірів. Здавалося б, цей критерій важко виразити числовим значенням, та без чисельної оцінки можна вибрати гарніший сувернір. Але такий вибір „без числа” можливий лише, якщо зразків мало. Якщо ж їх, наприклад, є 100, то при виборі, напевно, прийдеться застосовувати числа: зокрема, оцінку в балах. Така оцінка дуже недосконала, але все ж таки є неминучою.
Третя обов’язкова властивість критерію оптимізації: його величина повинна змінюватись монотонно при покращенні якості функціонування системи. Це означає, що оцінювати об’єкт можна за принципом: „чим більший критерій – тим краще”, або „чим менший критерій – тим краще”, але ні в якому разі – за принципом: „ось це значення критерію є оптимальним і відхилятись від нього не слід”.
В наведених формулюваннях оцінки „більше” чи „менше” не мають різниці. Вони визначаються фізичним змістом критерію. Добре, коли прибуток великий, але собівартість мала; коли велика продуктивність, але малі витрати. Помноживши будь-який критерій на (-1), ми перетворимо „більше” в „менше” і, навпаки.
Але ось критерій, що володіє деяким оптимальним значенням, від якого небажано відхилятись, не придатний. Наприклад, в лікувальній суміші вміст того чи іншого інградієнту не може бути критерієм оптимізації: інакше ми б отримали не суміш заданого складу, а максимальну концентрацію однієї речовини.
Якщо для якогось параметру, що характеризує систему, існує оптимальне значення, то цей параметр – не критерій оптимізації, а оптимізуючий фактор.
Обмеження. Як би добре не був вибраний критерій оптимізації, цього в більшості задач недостатньо, щоб врахувати всі умови, в яких повинен відбуватися процес. З однієї сторони, як вже зазначалось (див. приклад 1), нас завжди цікавить не один, а багато результатів процесу. З іншої сторони, ніколи не вдається реалізувати всі бажані значення вхідних параметрів. Умови, яких необхідно дотримуватись незалежно від того, як їх виконання вплине на величину критерію оптимізації, називають обмеженнями.
Приклад 5. Обмеження і необмеження.
В звіті про наукову роботу вказано, що синтез досліджений в температурному інтервалі від 363 К до 383 К. Нижня межа визначалась тим, що при подальшому зниженні температури суміш сильно загусла і її не вдалось перемішати. Верхня межа визначалась тим, що подальше зростання температури приводить до різкого зменшення падіння виходу продукту.
З точки зору формулювання задачі оптимізації (якщо за критерій оптимізації прийняти вихід продукту), нижня межа – обмеження, незалежно від того, як зниження температури впливає на вихід продукту. При цьому охолоджувати суміш не можна внаслідок зростання в’язкості. А ось верхню межу не варто вважати обмеженням. Дослідники заперечили високотемпературний режим не тому, що не могли його досягнути, а внаслідок несприятливого впливу зазначеного режиму на вихід продукту. Тут немає необхідності в понятті обмеження: заперечити високотемпературні режими можна безпосередньо за величиною критерію оптимізації.
Найчастіше обмеження виникають з таких причин:
- за кількістю і якістю сировини і продукції: склад сировини, як правило, задається не нами і змінювати його не можна; кількість сировини також може бути обмежена; випуск продукції не повинен бути меншим від планового і більшим за той, що можна реалізувати;
- за умовами технології: витрата повітря не може перевищувати продуктивність вентилятора; температура не може бути вищою за ту межу, при якій руйнується матеріал апарата чи каталізатор; розміри апаратів змінювати не можемо тощо;
- за економічними і кон’юктурними міркуваннями: капітальні витрати не повинні перевищувати виділеної суми; термін введення нового виробництва повинен відповідати запланованому періоду; не можна порушувати міжнародне патентно-ліцензійне законодавство;
- за міркуваннями гарантованого виконання вимог техніки безпеки, охорони праці, захисту довкілля та безпеки життєдіяльності – надзвичайно важлива велика група відповідних обмежень.
Крім цієї класифікації, обмеження можна розрізняти за формально-математичними ознаками. Так, виділяють обмеження типу рівностей і типу нерівностей.
Обмеження типу рівностей встановлюють визначене значення того чи іншого фактора:
hi=ai. (80)
Частіше всього фактор hi можна розглядати як один з контролюючих нерегулюючих входів (рис. 70). Так, за конкретних умов роботи задаються відповідні чисельні значення, характеризуючи склад сировини, розміри апаратів, завантаження в апарати тощо.
Обмеження типу нерівностей визначають межі, за яких допустима зміна параметрів f процесу:
. (81)
Два перших обмеження (81) задають односторонні межі (наприклад, продуктивність не нижче заданої, температура не вище тієї, на яку розрахований матеріал). Третє обмеження (81) – задає двосторонні межі (наприклад, температура в межах від температури замерзання до температури кипіння).
В математичних процедурах знаходження оптимуму відіграє суттєву роль розподіл обмежень за такими ознаками: обмеження 1-го роду – умови (80) або (81), де в якості параметрів h i f фігурують вхідні фактори; в обмеженнях 2-го роду ці параметри – різні функції входів (наприклад, вихідні показники або температури в деяких точках всередині апарата). Коли при певному математичному розв’язку задачі розглядається відповідний режим, то він задається значеннями входів. При цьому питання про те, чи не порушені відповідні обмеження 1-го роду, перевіряється безпосередньо. А для перевірки дотримання обмежень 2-го роду необхідно спочатку розрахувати відповідні параметр-функції, що може ускладнити розрахунок.
Оптимізуючі фактори – це ті з входів системи (рис.68), які в процесі оптимізації відносять до керуючих. Це ті впливи, які ми застосовуємо для оптимізації процесу. Інші фактори при цьому не регулюються, хоча їх значення враховують при визначенні оптимальних умов: ці фактори фігурують в задачі в якості обмежень типу рівностей.
Число оптимізуючих факторів залежить від того, на якій стадії розробки виробництва здійснюється оптимізація. Якщо виробництво ще проектується (оптимальне проектування), то до числа оптимізуючих факторів доцільно віднести якомога більше число відповідних факторів. Дійсно, на цій стадії регулювати фактори дуже просто: регулювання (зміна значень) здійснюється не в реальній дійсності, а на математичній моделі. Тому тут бажано знайти оптимальні значення максимального числа факторів.
Рис. 68. Схема зовнішніх зв’язків систем
Але задача оптимізації виникає і після пуску виробництва (оптимальне керування). При цьому число оптимізуючих впливів стає суттєво меншим. Частину факторів ми вже не можемо змінювати (наприклад, такими факторами є розміри апаратів). Але і не всі інші фактори доцільно тепер регулювати. Справа в тому, що чим більше керуючих факторів, тим складніша система керування, складніша її математична модель. При великій кількості факторів вона може стати настільки складною, що ЕОМ, яка розраховує оптимальні режими, не зможе встигати за зміною умов перебігу процесу: рекомендації з оптимізації прийдуть, коли їх реалізація вже запізниться. Все це диктує використати для оптимального керування порівняно невелику кількість факторів.
Цільова функція – це те саме, що критерій оптимізації, але це є критерій, що розглядається як функція вхідних факторів:
F=F(x1, x2,…, xn, h1,…,hm). (82)
Чим більше (чи чим менше) значення F, тим краще. Тому можна дати таке визначення оптимуму: оптимум – це екстремум (максимум чи мінімум) цільової функції. Ті значення факторів хj, за яких досягається оптимум, називають оптимальними значеннями. Таким чином, математично задача оптимізації формулюється як задача знаходження екстремуму.
При цьому в точці екстремуму необхідно дотримуватись всіх обмежень. Тому в багатьох випадках оптимум необхідно шукати на краю області допустимих значень, за межі якої не можна вийти внаслідок наявності відповідних обмежень (рис. 69). На рис. 69 відрізок ab є областю допустимих значень, що визначається обмеженням a ≤ x ≤ b.
Методи знаходження точки оптимуму можна розділити на такі три основні групи.
Рис. 69. Графік, що ілюструє оптимум на краю області
допустимих значень
1. Аналітичні методи. Їх застосовують, коли ми можемо продиференціювати цільову функцію і шукати екстремум, виходячи з умови рівності нулю відповідних похідних.
2. Чисельні або пошукові методи. Для їх застосування потрібно, щоб цільова функція була обраховуваною: повинен бути відомий алгоритм, за яким можна розраховувати значення критерію оптимальності при заданих значеннях відповідних факторів.
3. Методи, що застосовуються, якщо цільова функція необраховувана. Практично, це означає, що вигляд функції невідомий. Тоді залишається лише одне: планувати і реалізувати експеримент так, щоб в кінцевому підсумку досягнути області оптимуму. Це – експериментальна оптимізація, що складає важливий розділ планування експерименту.
Особлива група задач оптимізації – задачі, в яких критерій оптимізації є не функцією, а функціоналом. Так буває, якщо критерій залежить не від значення яких-небудь факторів, а від характеру безперервної зміни цих факторів: наприклад, якщо перебіг перехідного процесу визначається безперервною зміною керуючого впливу в часі, або якщо склад суміші на виході з апарату ідеального витіснення визначається профілем температури вздовж всього апарату. В таких задачах використовують варіаційні методи (варіаційне обрахування, динамічне програмування, принцип максимуму).
