Цель: Составить план перевозок горючего, минимизирующий общую сумму транспортных расходов.
Задача: В пунктах А и В находятся соответственно 150 и 90 т горючего. Пунктам 1, 2, 3 требуются соответственно 60, 70, 110 т горючего. Стоимость перевозки 1 т горючего из пункта А в пункты 1, 2, 3 равна 60, 10, 40 тыс. руб. за 1 т соответственно, а их пункта В в пункты 1, 2, 3 – 120, 20, 80 тыс. руб. за 1 т соответственно. Составить план перевозок горючего, минимизирующий общую сумму транспортных расходов.
Транспортная задача закрытого типа, так как запасы поставщиков и суммарный спрос потребителей одинаковы.
Экономико-математическая модель задачи:
Пусть – Xij- объем перевозки от i- го поставщика j-ому потребителю.
| Потребители Вj | В1 | В2 | В3 | Запасы пост. | |||
| Поставщики Ai | |||||||
| А1 | X11 | X12 | X13 | ||||
| А2 | X21 | X22 | X23 | ||||
| Спрос потр. |
Запасы на базах и спрос потребителей накладывают ограничения на переменную Xij.
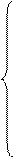
Х11 + Х12 + Х13 = 150
Х21 + Х22 + Х23 = 90
(1) Х11 + Х21 = 60
Х12 + Х22 = 70
Х13 + Х23 = 110
Составим целевую функцию:
(2) Z = 60X11 + 10X12 + 40X13 + 120 X21 + 20X22 + 80X23 → min
Таким образом, на множестве неотрицательных решений, системы ограничений (1) найдем такое решение
Х11 Х12 Х13
Х = Х21 Х22 Х23 ,
при котором целевая функция (2) принимает наименьшее значение.
Занесем данные в транспортную таблицу:
| Ui | Потребители Вj | В1 | В2 | В3 | Запасы пост. | |||
| Поставщики Ai | ||||||||
| U1= | А1 | |||||||
| U2= | А2 | |||||||
| Спрос потр. | ||||||||
| Vj | V1= | V2= | V3= |
Найдем первый опорный план поставок. Для этого воспользуемся методом наименьших затрат. Найдем в таблице клетку с наименьшим тарифом. Это клетка (1, 2). ЕЕ тариф С12 = 10. Дадим в эту клетку максимально возможную поставку. Х12 = min (150, 70) = 70. Клетку (2, 1) вычеркиваем (в эту клетку поставок давать не будем), т.к. потребность второго пункта полностью удовлетворена. Находим следующую клетку с наименьшим тарифом. Это клетка (1, 3), ее тариф С13 = 40. Дадим в эту клетку максимально возможную поставку. Х13 = min (150 – 70, 110) = 80. Клетку (1, 1) вычеркиваем (в эту клетку поставок давать не будем), т.к. запас первого поставщика (пункт А) полностью использован. Находим следующую клетку с наименьшим тарифом. Это клетка (2, 3), ее тариф С23 = 80. Дадим в эту клетку максимально возможную поставку. Х23 = min (110 – 80, 90) = 30. И в последнюю свободную клетку (2, 1) даем поставку 60.
Проверяем баланс по строкам и столбцам (соответствующие суммы).
Т.О. получен первый опорный план поставок. Полученный план невырожденный, т.к. число занятых клеток равно рангу системы. Ранг системы вычисляется по формуле: r = m + n – 1, где m – число поставщиков, n – число потребителей.
r = 2 + 3 – 1 =4, число занятых клеток р = 4.
Х1 = 0 70 80
60 0 30
Z1 = 70*10 + 80*40 + 60*120 + 30*80 = 13500 руб.
Проверим, будет ли полученный план оптимальным. Для этого воспользуемся методом потенциалов. Обозначим потенциалы поставщиков Ui, а потенциалы потребителей Vj. Для нахождения этих потенциалов составим систему уравнений по формуле Ui + Vj = Сi j, где Сi j – тариф занятой клетки.
 |
U1 + V2 = 10 Эта система имеет бесконечное множество решений.
U1 + V3 = 40 Найдем одно их них. Положим U1 = 0. Тогда V2 = 10,
U2 + V1 = 120 V3 = 40, U2 = 40, V1 = 80.
U2 + V3 = 80
| Ui | Потребители Вj | В1 | В2 | В3 | Запасы пост. | |||
| Поставщики Ai | ||||||||
| U1=0 | А1 | — | ||||||
| U2=40 | А2 | — | ||||||
| Спрос потр. | ||||||||
| Vj | V1=80 | V2=10 | V3=40 |
Далее, оценим свободные клетки по формуле: Di j = Сi j – (Ui + Vj), где Сi j – тариф свободной клетки.
D11 = 60 – (0 + 80) = - 20 ≤ 0, D22 = 20 – (40 + 10) = - 30 ≤ 0
Среди оценок свободных клеток есть отрицательные. Это значит, что полученный план не является оптимальным. Поэтому надо перераспределить поставки в одну из этих свободных клеток (с отрицательной оценкой). Перераспределим поставки в клетку (1, 1) (отрицательная оценка по модулю меньше). Для этого введем несколько определений.
Циклом называется последовательность клеток, в которой две и только две клетки находятся в одной строке или в одном столбце, причем последняя клетка цикла находится в той же строке или столбце, что и первая клетка.
Циклом пересчета называется такой цикл в таблице с базисным распределением поставок, при котором одна из его вершин лежит в свободной клетке, остальные – в заполненных.
Цикл пересчета называется означенным, если в его вершинах расставлены знаки «+» и «−», так, что в свободной клетке стоит знак «+», а соседние вершины имеют противоположные знаки «−».
НАПРИМЕР
| — | — |   70 +
|  120 ‒
| — |
 — + *
| 20 ‒ | — | ||
| — |  60 ‒
| — | 50 + | — |
| — | — |  —
| — |
| — |  — *
|  120
| — | |
 —
| — | |||
| — |  60
| — | — | |
| — | — | — | — |
Построим для клетки (1, 1) означенный цикл пересчета:
+ −
* 80
Величина пересчета λ = min (60, 80) = 60.
− 60 30 +
Эту величину добавляют в клетки положительного полуцикла и вычитают в клетках отрицательного полуцикла. После пересчета по циклу строим новую транспортную таблицу, при этом значения потенциалов берем новые.
| Ui | В1 | В2 | В3 | Запасы пост. | ||||
| U1= | А1 | |||||||
| U2= | А2 | — | — | |||||
| Спрос потр. | ||||||||
| Vj | V1= | V2= | V3= |
Полученный план невырожденный, т.к. число занятых клеток равно рангу системы.
Х1 = 60 70 20
0 0 90
Z1 = 60*60 + 70*10 + 20*40 + 90*80 = 12300 руб.
Проверим, будет ли полученный план оптимальным. Для этого воспользуемся методом потенциалов.
Для нахождения новых потенциалов составим систему уравнений по формуле Ui + Vj = Сi j, где Сi j – тариф занятой клетки.
U1 + V1 = 60 Эта система имеет бесконечное множество решений.
U1 + V2 = 10 Найдем одно их них. Положим U1 = 0. Тогда V1 = 60,
U1 + V3 = 40 V2 = 10, V3 = 40, U2 = 40,.
U2 + V3 = 80
| Ui | В1 | В2 | В3 | Запасы пост. | ||||
| U1=0 | А1 | |||||||
| U2=40 | А2 | — | — | |||||
| Спрос потр. | ||||||||
| Vj | V1=60 | V2=10 | V3=40 |
Далее, оценим свободные клетки по формуле: Di j = Сi j – (Ui + Vj), где Сi j – тариф свободной клетки.
D21 = 120 – (40 + 60) = 20 ≥ 0, D22 = 20 – (40 + 10) = - 30 ≤ 0
Среди оценок свободных клеток есть отрицательная. Это значит, что полученный план не является оптимальным. Поэтому надо перераспределить поставки в одну из этих свободных клеток (с отрицательной оценкой). Перераспределим поставки в клетку (2, 2) (отрицательная оценка).
Построим для клетки (2, 2) означенный цикл пересчета:
− +
70 20
Величина пересчета λ = min (70, 90) = 70.
+ * 90 −
Эту величину добавляют в клетки положительного полуцикла и вычитаются в клетках отрицательного цикла. После пересчета по циклу строим новую транспортную таблицу, при этом значения потенциалов берем новые.
| Ui | В1 | В2 | В3 | Запасы пост. | ||||
| U1=0 | А1 | — | ||||||
| U2=40 | А2 | — | ||||||
| Спрос потр. | ||||||||
| Vj | V1=60 | V2= - 20 | V3=40 |
Полученный план невырожденный, т.к. число занятых клеток равно рангу системы.
Х1 = 60 0 90
0 70 20
Z1 = 60*60 + 90*40 + 70*20 + 20*80 = 10200 руб.
Проверим, будет ли полученный план оптимальным. Для этого воспользуемся методом потенциалов.
Для нахождения новых потенциалов составим систему уравнений по формуле Ui + Vj = Сi j, где Сi j – тариф занятой клетки.
U1 + V1 = 60 Эта система имеет бесконечное множество решений.
U1 + V3 = 40 Найдем одно их них. Положим U1 = 0. Тогда V1 = 60,
U2 + V2 = 20 V2 = - 20, V3 = 40, U2 = 40,.
U2 + V3 = 80
Далее, оценим свободные клетки по формуле: Di j = Сi j – (Ui + Vj), где Сi j – тариф свободной клетки.
D21 = 120 – (40 + 60) = 20 ≥ 0, D12 = 10 – (0 + (- 20)) = 30 ≥ 0.
Среди оценок свободных клеток нет отрицательных. Все оценки положительны. Это значит, что полученный план оптимален.
Хопт = 60 0 90
0 70 20
Zопт = 60*60 + 90*40 + 70*20 + 20*80 = 10200 руб.
Экономический анализ. Общая сумма транспортных расходов будет минимальной и составит 10200 руб., если перевозку горючего запланировать следующим образом: из пункта А доставить в пункт 1- 60 тонн горючего, в пункт 3 – 90 тонн; из пункта В отправить в пункт 2- 70 тонн, в 3 пункт – 20 тонн горючего. При этом запасы в пунктах А и В полностью реализованы и потребности пунктов 1, 2 и 3 будут удовлетворены.
