При замыкании ключа ток начинает увеличиваться, в катушке возникает ЭДС самоиндукции, которая по правилу Ленца старается уменьшить ток. Ток уменьшается постепенно по закону переходного процесса.
(1)
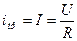
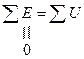
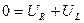
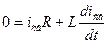
Из математики известно, что дифференциальное уравнение с разделяющимися переменными имеет решением экспоненту:
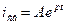, где
A — постоянная интегрирования;
p — корень характеристического уравнения цепи.
Чтобы найти p, надо составить характеристическое уравнение цепи по правилу:
вместо функции ставят единицу, а вместо производной — букву p:
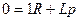
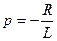
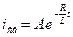
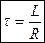
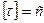
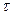— постоянная цепи RL
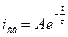
Чтобы найти постоянную интегрирования A, применяем I закон коммутации:
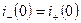
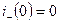
Чтобы найти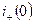 
, надо в уравнение (1) подставить 
:
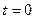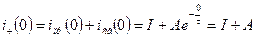
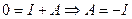
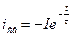
Решение:
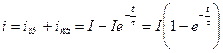
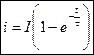— уравнение тока при включении цепи RL на постоянное напряжение
Практически переходной процесс заканчивается через время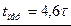 
.
Вывод: чем больше постоянная времени, тем медленнее идёт переходной процесс.
Построим график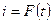 
:
Подставим в уравнение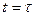 
:
Физический смысл 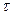при включении цепи RL на постоянное напряжение:
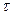— время, за которое ток достигает значения 0,63 от установившегося.
Анализ процессов при коротком замыкании последовательной RL-цепи классическим методом
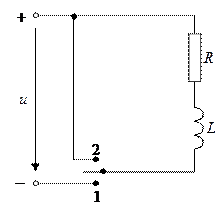
В первом положении ключа по цепи течёт ток. Во 2 положении цепь закорачивается проводом, и ток начинает уменьшаться. В катушке возникает ЭДС самоиндукции, которая по правилу Ленца поддерживает ток, и ток постепенно уменьшается по закону переходного процесса.
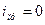
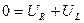
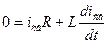
Получим уравнение, аналогичное предыдущему, поэтому и его решение аналогично:
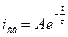, где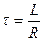 
Чтобы найти A, надо применить I закон коммутации:
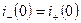
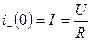
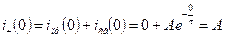
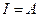, тогда
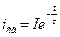
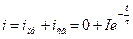
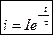— уравнение тока при коротком замыкании цепи RL
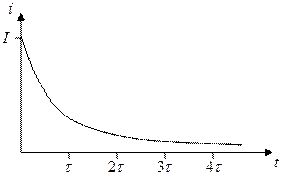
Подставим в уравнение :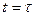
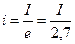
Физический смысл 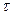при коротком замыкании цепи RL:
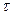— время, за которое ток цепи уменьшается в 2,7 раза по сравнению с первоначальным.
Анализ процессов заряда конденсатора классическим методом
При замыкании ключа конденсатор заряжается до напряжения источника по закону переходного процесса.
(1)
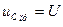
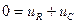
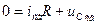
Получим дифференциальное уравнение с разделяющимися переменными, решение которого экспонента:
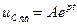
Чтобы найти p, составляем характеристическое уравнение цепи:
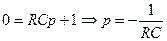
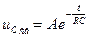
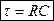— постоянная времени цепи RC
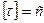
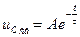
Чтобы найти постоянную интегрирования A, применим II закон коммутации:
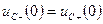
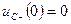
Чтобы найти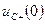 
, в уравнение (1) подставляем :
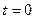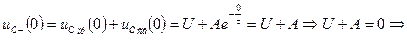
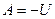
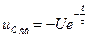
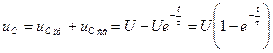
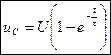— уравнение напряжения на конденсаторе при его заряде
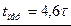
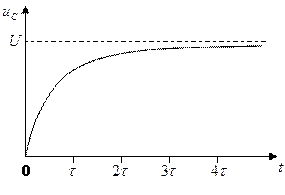
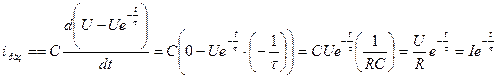
Подставим в уравнение :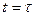
Физический смысл 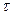времени при заряде конденсатора:
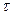— время, за которое напряжение на конденсаторе достигает значения 0,63 от установившегося.
