Цепь с R
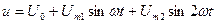
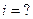
Расчёт таких цепей происходит методом наложения.
Каждая гармоника рассчитывается отдельно, а затем находят общий ток как сумму токов отдельных гармоник.
Величина сопротивления R для всех гармоник одинакова, поэтому форма тока будет такой же, как форма напряжения на входе. Чтобы найти его, необходимо просто каждую гармонику напряжения разделить на величину R. Фаза остаётся той же, т. к. в цепи с R напряжение и ток совпадают по фазе.
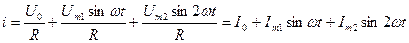
Цепь с катушкой
С ростом частоты индуктивное сопротивление растёт, поэтому катушка хорошо пропускает токи НЧ (нижних частот) и плохо токи ВЧ (верхних частот). Катушка — фильтр нижних частот.
Форма тока будет более сглаженной, чем форма напряжения на входе.
Порядок расчёта:
1. Рассчитываем индуктивное сопротивление каждой гармоники:
2. По закону Ома рассчитываем максимальное значение каждой гармоники:
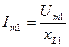
3. Учитывая, что в цепи с L ток отстаёт от напряжения на угол 90°, записываем уравнение тока каждой гармоники:
4. Записываем уравнение общего тока, как сумму токов отдельных гармоник:
Цепь с конденсатором
С ростом частоты емкостное сопротивление уменьшается, поэтому конденсатор хорошо пропускает токи ВЧ и плохо токи НЧ. Конденсатор — фильтр верхних частот.
Форма тока будет более несинусоидальной, чем форма напряжения на входе.
1. 
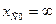(конденсатор не пропускает постоянный ток)
2. 
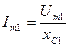
3. В цепи с C ток опережает напряжение на угол 90°, поэтому
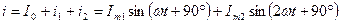
5. Методика расчёта электрических цепей при негармоническом воздействии (на примере)
Расчёт цепей с несинусоидальными токами ведётся символическим методом (комплексными числами).
Задача
Дано:
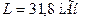
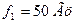
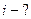
Рассчитать 
. Построить спектр в масштабе.
- Определяем комплексное сопротивление каждой гармоники:
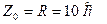
- Находим комплексную амплитуду тока каждой гармоники:
- От комплексов переходим к уравнениям
Общее уравнение:
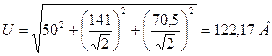
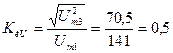
6. Соединение обмоток генератора и сопротивлений нагрузки звездой. Схема соединения, фазные и линейные токи и напряжения, соотношение между ними. Расчёт трёхфазной электрической цепи при соединении приёмника звездой. Мощность трёхфазной цепи при симметричной нагрузке. Роль нейтрального провода
Трёхфазные цепи
Трехфазная цепь состоит из трёх однофазных цепей, в которых действует три одинаковые по амплитуде и частоте ЭДС, сдвинутые по фазе друг относительно друга на угол 120°.
Фазы трёхфазной системы обозначаются A, B, C.
Обмотки трёхфазного генератора и сопротивления нагрузки могут соединяться по схеме 
или 
(звезда или треугольник).
Соединение обмоток генератора и сопротивлений нагрузки звездой
При таком соединении все концы обмоток соединяются в одну общую точку, которую называют нейтральной или нулевой.
Рассматриваем симметричную нагрузку 
.
Начало фаз генератора и нагрузки соединяются проводами, которые называются линейными.
(линейный ток)
Ток, текущий по линейному проводу называется линейный, а ток, текущий в сопротивления нагрузки, называется фазным.
Из схемы видно, что при соединении звездой 
.
Напряжение между началом и концом сопротивления нагрузки называется фазным.
Напряжение между соседними линейными поводами называется линейным.
Запишем уравнение по II закону Кирхгофа:
Построим эти уравнения на векторной диаграмме.
При симметричной нагрузке фазные напряжения равны и сдвинуты по фазе на угол 120°, как фазные ЭДС.
По правилу векторного вычитания получаем 
.
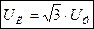
Если нагрузка чисто активная (R), то фазный ток совпадает по фазе с фазным напряжением.
Если нагрузка несимметричная, то нулевые точки источника и нагрузки соединяются проводом, который называется нейтральным или нулевым. По этому проводу потечёт ток, и напряжение на фазах нагрузки останутся одинаковыми.
Порядок расчёта
Расчёт ведётся для одной фазы симметричной нагрузки:
1. Определяем сопротивление фазы
2. Закон Ома справедлив только для фазных значений
3. 
4. 
, где 
.
7. Соединение обмоток генератора и сопротивлений нагрузки треугольником. Схема соединения, фазные и линейные токи и напряжения, соотношение между ними. Расчёт трёхфазной электрической цепи при соединении приёмника треугольником. Мощность трёхфазной цепи при симметричной нагрузке
При таком соединении конец первой обмотки соединяется с началом второй, конец второй — с началом первой, а конец третьей — с началом первой.
Места соединения обмоток и нагрузки соединяются линейными проводами.
Из схемы видно, что при соединении треугольником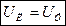 
.
Составим уравнение по I закону Кирхгофа:
Построим векторную диаграмму для симметричной чисто активной нагрузки.
Напряжение будем строить в виде треугольника линейных напряжений.
Т. к. нагрузка чисто активная, то фазный ток совпадает по фазе с фазным напряжением.
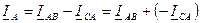
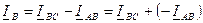
Выведем формулу для 
:
.
При соединении треугольником 
.
Расчёт симметричной трёхфазной системы при соединении треугольником:
1.
2. Закон Ома только для фазных значений:
, где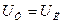 
3. 
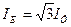
4. .
Получить трёхфазную систему ЭДС можно с помощью трёхфазного генератора, который имеет статор — неподвижную часть и ротор — движущуюся часть. В статоре расположены 3 одинаковые обмотки, оси которых сдвинуты в пространстве на угол 120°. На роторе имеется обмотка постоянного тока, вокруг которой образуется магнитное поле. При вращении ротора вращающееся магнитное поле сначала пересекает обмотку A, затем обмотку B, а затем — C. В результате в обмотках образуется ЭДС ЭМИ (электромагнитной индукции), сдвинутые по фазе на угол 120°.
Идеальный и реальный колебательные контура. Основные характеристики колебательного контура (свободные колебания, частота и период свободных колебаний, характеристическое сопротивление, добротность)
Контур состоит из катушки и конденсатора. Идеальный колебательный контур состоит из катушки и конденсатора, но в нём нет сопротивления потерь.
В 1 положении ключа конденсатор заряжается до напряжения источника, в нём накапливается энергия электрического поля 
.
Во 2 положении конденсатор начинает разряжаться на катушку, и энергия переходит в энергию магнитного поля катушки 
.
В катушке возникает ЭДС самоиндукции, которая поддерживает ток, и конденсатор снова заряжается, но в другом направлении. Энергия опять переходит в энергию электрического поля конденсатора.
Вывод: конденсатор и катушка обмениваются энергией, т. е. происходит колебание энергии. Такие колебания называются собственными или свободными, т. к. происходят без помощи источника от первоначального запаса энергии.
Эти колебания будут незатухающими. Их амплитуда мс течением времени не будет уменьшаться, т. к. нет сопротивления потерь, и энергия из контура не уходит. Выведем формулу частоты и периода свободных колебаний:
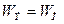
Вывод: частота и период свободных колебаний зависят от L и C, но не зависят от величины приложенного напряжения.
Рассчитаем сопротивление катушки и конденсатора на частоте свободных колебаний.
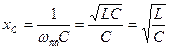
Вывод: сопротивление катушки и конденсатора на частоте свободных колебаний называется характеристическим:
В реальном контуре существует сопротивление потерь, поэтому колебания будут затухающими, их амплитуда с течением времени будет уменьшаться, т. к. часть энергии будет уходить через сопротивление потерь.
Отношение характеристического сопротивления к резистивному называется добротность:
(безразмерная)
В обычных контурах она составляет единицы – десятки.
Добротность характеризует качество контура. Чем выше добротность, тем медленнее происходят затухания. Величина, обратная добротности, обозначается d — затухание контура:
Принципиальная схема последовательного колебательного контура. Резонанс напряжений в последовательном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе напряжений. Резонансная частота, добротность. Настройка колебательного контура в резонанс
Резонанс напряжений
Колебания называются вынужденными, если они происходят под действием источника.
Контур называется последовательным, если катушка и конденсатор соединены последовательно с источником:
Резонансом называется такое состояние цепи, когда ток и напряжение на входе совпадают по фазе, => 
.
В последовательном контуре возможен резонанс напряжений.
— условие резонанса напряжений (
).
Обычно все параметры цепи, относящиеся к резонансу, записываются с индексом 0, => сопротивление контура в момент резонанса
Сопротивление последовательного контура в момент резонанса минимально.
Свойства цепи при резонансе напряжений
1. 
При резонансе напряжений в контуре течёт максимальный ток.
2. 
При резонансе напряжений напряжения на идеальной катушке и конденсаторе равны.
3. 
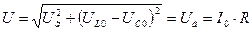
На практике 
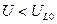и 
, => 
и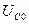 
Вывод: это явление и называется резонанс напряжений, потому что напряжение на идеальной катушке и конденсаторе больше, чем напряжение на входе в момент резонанса.
4. Нарисуем векторную диаграмму:
5. 
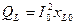
Выводы:
§ Т. к. 
, то от источника потребляется только активная мощность.
§ 
— катушка и конденсатор обмениваются энергией, а т. к. 
, то с источником обмена энергией не происходит.
Резонансная частота, добротность последовательного контура
Выведем формулу резонансной частоты:
Вывод: резонанс напряжений наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура 
.
Настроить контур в резонанс можно:
1) изменяя L или C, при этом подгоняем частоту собственных колебаний под частоту питающего напряжения;
2) можно изменять частоту питания, подгоняя её под частоту собственных колебаний контура.
Т. к. , то можно записать, что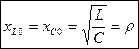 
.
Сопротивление катушки и конденсатора на резонансной частоте равно характеристическому сопротивлению контура.
Формула добротности:
Вывод: добротность в последовательном контуре показывает, во сколько раз напряжение на выходе больше, чем на входе в момент резонанса.
Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной
Расстройка — отклонение частоты от резонансной. Различают:
1) Абсолютная расстройка — разность текущей частоты и резонансной:
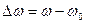
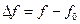
Расстройка может и положительной и отрицательной.
2) Относительная расстройка — отношение абсолютной расстройки к резонансной частоте:
3) Обобщённая расстройка — отношение реактивного сопротивления x к резистивному:
Обычно входные характеристики строят от расстройки.
Входные АЧХ и ФЧХ последовательного контура
, где 
— формула входной АЧХ последовательного контура
(на резонансной частоте все расстройки равны 0)
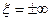
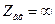
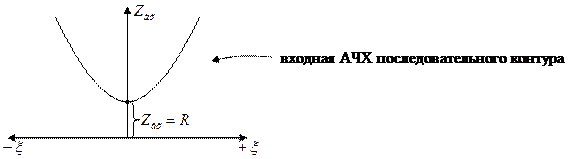
Вывод: на резонансной частоте сопротивление последовательного контура имеет наименьшее значение . По мере увеличения расстройки сопротивление контура возрастает.
ФЧХ:
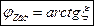— формула входной ФЧХ последовательного контура
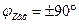
Вывод: на резонансной частоте последовательный контур имеет чисто активное сопротивление: . На частотах меньше резонансной характер сопротивления активно-емкостной, т. к. 
. На частотах больше резонансной характер сопротивления активно-индуктивный: 
.
Передаточные АЧХ и ФЧХ последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы
Обычно спектр частот радиосигнала составляет 2-3% от несущей частоты, поэтому можно приблизительно считать
— передаточная АЧХ последовательного контура в абсолютных координатах
Вывод: на резонансной частоте коэффициент передачи последовательного контура максимальный: .
ФЧХ:
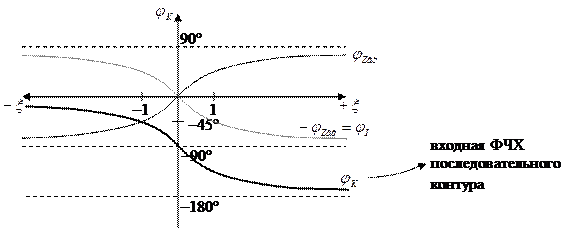
На выходе стоит конденсатор, поэтому напряжение выхода отстаёт от тока на 90°. Угол 
практически равен углу выходного напряжения, поэтому характеристику 
сдвигаем на 90° вниз:
Передаточная ФЧХ имеет линейный участок при расстройках от 
до 
.
Прохождение через колебательный контур сигналов негармонической формы. Избирательные свойства последовательного контура
Избирательность — способность цепи различать сигналы по частоте. Подадим на последовательный контур сигнал, который состоит из 5 гармоник одинаковой амплитуды.
На выходе амплитуда сигнала не резонансной частоте будет максимальной, т. к. 
, и на этой частоте самый большой коэффициент передачи.
Вывод: последовательный контур обладает избирательностью по напряжению. Он выделяет сигнал резонансной частоты.
Полоса пропускания контура — область частот, на границах которой модуль комплексного коэффициента передач уменьшается в 
раз по сравнению с резонансным.
На уровне полосы пропускания коэффициент обозначается 
:
Нарисуем передаточную характеристику 
:
Вывод: чем выше добротность, тем уже полоса пропускания контура.
1) 
2) 
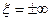
Кривые тока и напряжения такого вида называются резонансными.
Примечание:
При малых расстройках напряжение на катушке и конденсаторе можно рассчитать по формуле:
Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность
Контур называется параллельным, если катушка, конденсатор и источник соединены параллельно.
В параллельном контуре может возникнуть резонанс токов, когда напряжение и ток на входе совпадают по фазе: .
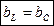— условие резонанса токов
Проводимость индуктивная равна проводимости емкостной.
При резонансе токов сопротивление параллельного контура максимально.
Свойства цепи при резонансе токов:
1. Ток в момент резонанса:
При резонансе токов общий ток минимальный.
2. На практике 
,
При резонансе токов токи ветвей приблизительно равны.
3. Построим векторную диаграмму для резонанса токов:
Если бы 
(контур идеальный), то токи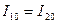 
, и общий ток был бы равен 0, но т. к. есть небольшое 
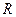, то существует активная составляющая тока (маленькая) и общий ток равен этой активной составляющей.
4. Выведем формулу резонансной частоты. Для этого 
Вывод: резонанс токов наступает тогда, когда частота питающего напряжения равна частоте собственных колебаний контура.
Получить резонанс токов можно, изменяя L или C, или частоту питающего напряжения.
5. Энергетический процесс при резонансе токов такой же, как и при резонансе напряжений:
Рассчитаем токи в момент резонанса:
Вывод: добротность в параллельном контуре показывает, во сколько раз токи ветвей больше общего тока в момент резонанса, поэтому это явление и называется резонанс тока.
