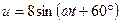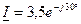Параллельные цепи RL и RC при гармоническом воздействии
Для параллельных цепей начинаем строить векторную диаграмму с вектора напряжений.
отстаёт от напряжения на угол 
, т. к. цепь RL.
опережает напряжение на угол 
, т. к. цепь RС.
Общий ток равен векторной сумме этих токов:
Чтобы найти общий ток, существует специальный метод расчёта — метод составляющих токов.
Разложим ток на две составляющие:
— активная составляющая, совпадает по фазе с напряжением;
— индуктивная составляющая, отстаёт от напряжения на угол 90°.
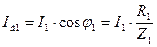
Разложим ток на составляющие:
— активная составляющая, совпадает по фазе с напряжением;
— емкостная составляющая, опережает напряжение на угол 90°.
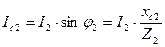
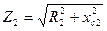
Из треугольника ABC:
Проводимости при гармоническом воздействии
Отношение активной составляющей тока к напряжению, называется активной проводимостью:
Отношение индуктивной (емкостной) составляющей тока к напряжению, называется реактивной проводимостью:
Отношение тока ветви (общего тока) к напряжению называется полной проводимостью:
Разделим все стороны диаграммы токов на напряжение, получим диаграмму проводимостей:
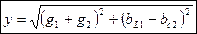
Если параллельно соединяется по одному элементу, то формулы проводимостей упрощаются. Проводимость будет обратно пропорциональна сопротивлению:
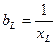
Чтобы записать входное сопротивление цепи в комплексной (символической) форме, используют обычную формулу сопротивления при параллельном соединении, только вместо сопротивлений подставляют их комплексные выражения:
В числитель подставляем в показательной форме, в знаменатель — в алгебраической.
Вопрос 37. Представление напряжения и тока в комплексной форме. Отрицательные углы. Законы Ома и Кирхгофа в комплексной форме. Выражение мощности в комплексной форме. Цепь с произвольным числом резистивных и реактивных элементов. Построение векторной диаграммы.
Выражение тока и напряжения в комплексной (символической) форме
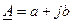
Рассмотрим перевод комплексных чисел из алгебраической формы в показательную.
Дано: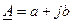
Определить:
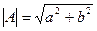
Если мнимая часть отрицательна, то угол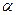 
также отрицателен.
Рассмотрим перевод обратно:
Дано:
Определить: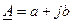
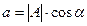
Если угол 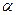отрицателен, то мнимая часть будет отрицательной.
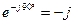
Примеры:
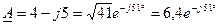
Выражают ток и напряжение в показательной форме. Модуль равен максимальному или действующему значению, аргумент равен начальной фазе:
Например:
