На практиці часто приходиться на основі результатів випробувань (вибірки) знати закон розподілу генеральної сукупності. Якщо закон розподілу невідомий, але є підстава вважати, що він має певний вигляд (наприклад назвемо його R), то висувають гіпотезу: генеральна сукупність розподілена за законом R, тобто в цій гіпотезі мова йтиме про вигляд передбаченого розподілу.
Можливі випадки, коли закон розподілу відомий, але його параметри невідомі. Якщо є підстава припустити, що його невідомий параметр а рівний певному значенню а0, то висувають гіпотезу: а= а0; в цьому випадку гіпотеза припускає оцінку параметру конкретного розподілу.
Можливі й інші гіпотези: про рівність параметрів двох чи декількох розподілів, про незалежність вибірок, про значимість вибіркового коефіцієнта кореляції тощо.
Статистичною називають гіпотезу про вигляд невідомого розподілу або про параметри невідомих розподілів. Наприклад, статистичними є гіпотези:
1) генеральна сукупність розподілена за нормальним законом;
2) коефіцієнт кореляції генеральної сукупності системи (х, у), розподіленої нормально, відмінний від нуля.
Перевірку гіпотез на основі вибіркових статистичних даних називають статистичною перевіркою гіпотез.
Одну з висунутих гіпотез виділяють в ролі основної і позначають, як правило Н0 (нульова), поряд з нею висувають альтернативну (конкуруючу) гіпотезу, яка суперечить основній і позначають Н1.
Наприклад, якщо нульова гіпотеза полягає в припущенні, що математичне сподівання певного розподілу mx рівне 5, то альтернативна гіпотеза, зокрема, може полягати в тому, що mx ¹ 5. Коротко це записують так:
Н0: mx = 5; Н1: mx¹ 5.
Розрізняють також гіпотези за кількістю припущень. Простою називається гіпотеза, що має лише одне припущення, інакше гіпотеза є складною, тобто складається зі скінченного чи нескінченного числа простих гіпотез.
Наприклад. Якщо l - параметр показникового розподілу, то гіпотеза Н0: l = 2 – проста. Якщо ж гіпотеза Н0: l > 5, то складна, бо складається з нескінченної множини простих гіпотез: Н1: l = аі, де аі – довільне число, більше l.
Очевидно, що на основі статистичних даних дуже важко, іноді і неможливо, робити безпомилкові висновки щодо гіпотез. В підсумку може бути прийняте неправильне рішення, тобто можуть бути допущені помилки двох родів.
Помилка першого роду полягає в тому, що буде відхилена правильна гіпотеза.
Помилка другого роду полягає в тому, що буде прийнята неправильна гіпотеза.
Правильне рішення може бути прийняте також у двох випадках:
а) гіпотеза приймається, причому і в дійсності вона правильна;
б) гіпотеза відхиляється, причому і в дійсності вона неправильна.
Ймовірність здійснити помилку першого роду позначають через a і називають її рівнем значимості. Число a задають малим і найчастіше використовують значення a, що дорівнюють 0,05; 0,001 і т.д. Якщо, наприклад, a=0,01, то це означає, що в одному випадку зі 100 є ризик допустити помилку першого роду (відхилити гіпотезу Н0).
Для перевірки нульової гіпотези використовують спеціально підібрану випадкову величину, точний чи наближений розподіл якої відомо. Цю величину позначають через Ф, якщо вона розподілена нормально, F – по закону Фішера-Снедекора, Т – по закону Стьюдента, c2 – по закону “хі квадрат” і т.д. оскільки зараз конкретний вигляд розподілу до уваги не береться, то позначають цю величину взагалі через К.
Статистичним критерієм (просто критерієм) називають випадкову величину К, що служить для перевірки нульової гіпотези. Для різних гіпотез ці критерії є різними.
Наприклад, а) коли перевіряють гіпотезу про рівність дисперсії двох нормальних генеральних сукупностей, то в ролі критерію К беруть відношення виправлених вибіркових дисперсій:
 .
.
Ця величина випадкова, тому в різних випробуваннях дисперсії приймають різні, наперед невідомі значення і розподілені за законом Фішера-Снедокора.
б) найбільш розповсюдженим критерієм перевірки гіпотези Н0 про закон розподілу ознаки генеральної сукупності є критерій узгодженості:
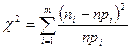
де m – число інтервалів, на які розбита вибірка, n – об’єм вибірки, ni – частота і-го інтервалу, rі – ймовірність попадання значень ознаки в і-ий інтервал, яка обчислюється для теоретичного закону розподілу.
Спостережуваним значенням Ксп називається значення критерію, обчислене по результатах вибірки.
§ 2. Критична область. Загальна методика побудови критичних областей
Всю множину значень статистичного критерію К можна розбити на дві підмножини, що не перетинаються А і Ā.
Значення статистичного критерію підмножини А Î W, при яких нульова гіпотеза приймається, називається областю прийняття гіпотези, а підмножина значень Ā, при яких гіпотеза Н0 відхиляється – критичною областю.
Основний принцип перевірки статистичних гіпотез формується так: якщо спостережуване значення критерію Ксп належить області прийняття гіпотези А – гіпотезу приймають, якщо Ксп належить критичній області Ā гіпотезу відхиляють.
Оскільки критерій К – одномірна випадкова величина, то всі її можливі значення належать деякому інтервалу. Тому область прийняття гіпотези А і критична область Ā також є інтервальними, а, значить, існують точки, котрі їх розділяють і називають критичними і позначаються kкр.
Розрізняють односторонню (правосторонню чи лівосторонню) і двосторонню критичні області (див.рис.1).

Рис. 1.
Правосторонньою називають критичну область, що визначається нерівністю К > kкр, де kкр – додатне число (рис. 1, а).
Лівосторонньою називають критичну область, що визначається нерівністю К < kкр, де kкр < 0 (рис. 1, б).
Двосторонньою називають критичну область, що визначається нерівністю К < k1кр, К > k2кр, де k2 > k1 (рис.1, в). зокрема, якщо критичні точки симетричні відносно нуля, двостороння критична область визначається нерівностями. Зокрема, якщо критичні точки симетричні відносно нуля, двостороння критична область визначається нерівностями К < - kкр, К > kкр, або ÷К÷ > kкр (kкр >0).
Перевірка статистичних гіпотез будь-якої природи здійснюється за такою схемою:
1. Формулюється статистична гіпотеза Н0.
2. Вибирається статистичний критерій відповідно до сформульованої нульової гіпотези Н0.
3. Залежно від гіпотези Н0 і альтернативної Н1 вибирається одностороння або двостороння критична область.
Щоб побудувати критичні області, необхідно знайти значення критичних точок.
В основі побудови критичної області лежить принцип практичної неможливості здійснитися малоймовірній випадковій події при одній спробі. Тому задається мала величина ймовірності a (a = 0,01; a = 0,05) (рівень значимості) критерію перевірки правильної гіпотези Н0: на основі відомого розподілу ймовірності критерію К визначається за допомогою спеціальних таблиць (див. додаток 1) критична точка kкр. По знайденому kкр відповідно відбудеться лівостороння, правостороння або двостороння критична область.
4. За результатами вибірки обчислюється спостережене значення критерію Ксп.
5. Виходячи з вимоги, що при правильності гіпотези Н0 ймовірність того, що Ксп потрапить у критичну область, має дорівнювати прийнятому рівню значимості a, перевіряється статистична гіпотези.
Це твердження подають для лівосторонньої критичної області так:
Р(К < kкр)= a,
для правосторонньої:
Р(К > kкр)= a,
для двосторонньої критичної області:
Р(К < k1кр) + Р(К > k2кр) = a.
На практиці двосторонню критичну область будують симетрично розміщену відносно нуля, розділяючи при цьому a порівну між кінцями критичних областей, тобто
Р(К < k1кр) = Р(К > k2кр) = a/2.
Якщо К потрапляє у критичну область, а ця подія малоймовірна і вона все-таки здійснилася, то нульова гіпотеза Н0 відхиляється. У протилежному разі – приймається.
Розглянемо декілька прикладів статистичної перевірки статистичних гіпотез.






