Нехай генеральні сукупності Х і У розподілені нормально, причому їх дисперсії відомі. З незалежних вибірок об’ємом nіm знайдемо середні вибіркові 
.
Потрібно по вибіркових середніх при заданому рівні значимості a перевірити нульову гіпотезу Н0, яка полягає в тому, що генеральні середні (математичні сподівання) даних сукупностей рівні між собою, тобто Н0: М[X] = М[Y].
Враховуючи, що вибіркові середні є незміщеними оцінками генеральних середніх, тобто 
, нульову гіпотезу можна записати так: Н0: М[ 
] = М[ 
], тобто перевірити, що математичне сподівання вибіркових середніх рівні між собою. Якщо гіпотеза Н0 правдива, то різниця між вибірковими середніми незначна.
В ролі критерію перевірки нульової гіпотези приймається випадкова величина
,
.
Критерій Z – нормована нормальна випадкова величина, бо є лінійна комбінація нормальних величин; Z – нормована, бо М (Z) = 0, s(Z) = 1 при справедливості гіпотези Н0.
Критична область будується в залежності від вигляду конкуруючої гіпотези.
Перший випадок. Нульова гіпотеза Н0: М[X] = М[Y], конкуруюча Н1: М[X] ¹ М[Y]. В цьому випадку будують двосторонню критичну область, виходячи з вимоги, що ймовірність попадання критерію в цю область, в припущенні справедливості нульової гіпотези, була рівна прийнятому рівні значимості a.
Найбільша потужність критерію (ймовірність попадання критерію в критичну область при правдивості конкуруючої гіпотези) досягається тоді, коли “ліва” і “права” критичні точки вибрані так, що ймовірність попадання критерію в кожен із двох інтервалів критичної області рівний a/2:
Р(Z < kлів кр) = a/2, Р(Z < kпр кр) = a/2.
Оскільки, Z – нормована нормальна величина, а розподіл такої величини симетричний відносно нуля, то критичні точки симетричні відносно нуля, тобто досить знайти праву границю, щоб знайти саму двосторонню критичну область (нехай kпр кр = kкр, kлів кр = - kкр).
Покажемо, як знайти kкр – праву межу двосторонньої критичної області, користуючись функцією Лапласа Ф(z). Відомо, що функція Лапласа визначає ймовірність попадання нормованої нормальної випадкової величини, наприклад, Z в інтервалі (0, z):
Р(0 < Z < z) = Ф(z). (1)
Так як розподіл Z симетричний відносно нуля, то Р(z Î [0, ¥)) = 0,5, то, якщо розбити цей інтервал kкр на інтервалі [0, kкр) È (kкр, ¥), то по теоремі додавання
Р(0 < Z < kкр) + Р (kкр < Z < ¥) = ½ (2)
Звідки Ф(kкр) + a/2 = 1/2
Ф(kкр) = 
(3)
Висновок І. Для того, щоб при заданому рівні значимості a перевірити нульову гіпотезу Н0: М[X] = М[Y] двох нормальних генеральних сукупностей з відомими дисперсіями при конкуруючій гіпотезі Н1: М[X] ¹ М[Y], потрібно обчислити
і по таблиці функції Лапласа знайти критичну точку рівності
Ф(kкр) = .
Якщо ÷Ксп÷ < kкр – нема підстави відхиляти нульову гіпотезу.
Якщо ÷Ксп÷ > kкр – нульову гіпотезу відхиляють.
Другий випадок. Нульова гіпотеза Н0: М[X] = М[Y], конкуруюча Н1: М[X] > М[Y].
В цьому випадку будують правосторонню критичну область, виходячи з вимоги, щоб ймовірність попадання критерію в цю область в припущенні справедливості нульової гіпотези була рівна прийнятому рівню значимості a:
Р(K > kкр) = a
Користуючись співвідношенням (2) Р(0 < Z < kкр) + Р (Z > kкр) = 1/2, маємо Ф(kкр) + a = 1/2 або Ф(kкр) = 
.
Висновок 2. Щоб при заданому рівні значимості a перевірити нульову гіпотезу Н0: М[X] = М[Y] при конкуруючій гіпотезі Н1: М[X] > М[Y], потрібно обчислити
і по таблиці функції Лапласа знайти критичну точку з рівності 
.
Якщо Kсп< kкр – нема підстави відхиляти нульову гіпотезу. Якщо Ксп> kкр – нульова гіпотеза відхиляється.
Третій випадок. Нульова гіпотеза H0: М[X]=M[Y]. Конкуруюча H1: M[X]<M[Y].
В цьому випадку будуть лівосторонню критичну область, виходячи з вимоги, що ймовірність попадання критерію в цю область, в припущенні справедливості нульової гіпотези, була рівна прийнятому рівню значимості:
.
Висновок 3. При конкуруючій гіпотезі M[X]<M[Y] треба обчислити Kсп і спочатку по таблиці функції Лапласа знайти “допоміжну точку” kкр з рівності , а потім покласти 
. Якщо Kсп>-kкр – немає підстави відхиляти нульову гіпотезу. Якщо Kсп<-kкр – нульову гіпотезу відхиляють.
Приклад 1. По двох вибірках, об’ємами n=40, m=50, взятих з нормальних генеральних сукупностей, знайдено вибіркові середні 
. Відомі генеральні дисперсії: D [X]=80, D [Y]=90. Потрібно при рівні значимості 0,01 перевірити нульову гіпотезу H0: M[X]=M[Y] при конкуруючій гіпотезі H1: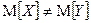 
.
Рішення. Знайдемо спостережувальний критерій
.
По умові конкуруючої гіпотези H1: критична область двостороння. Знайдемо праву критичну точку з рівності. По таблиці функції Лапласа (див.2, дод.1) знаходимо kкр=2,58. Так як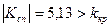 
, то згідно правила 1 нульова гіпотеза відхиляється, тобто генеральні середні різняться істотно.
