Метод узловых напряжений заключается в определении на основании первого закона Кирхгофа потенциалов в узлах электрической цепи относительно некоторого базисного узла. Базисный узел в общем случае выбирается произвольно, потенциал этого узла принимается равным нулю. Разность потенциалов рассматриваемого и базисного узлов называется узловым напряжением.
Положительное направление узловых напряжений указывается стрелкой от рассматриваемого узла к базисному.
Число уравнений, составляемое по методу узловых напряжений, равно
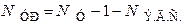
| (4.1) |
где 
– количество узлов цепи, 
– количество идеальных источников Э.Д.С.
Для произвольной схемы, содержащей 
узлов, система уравнений по методу узловых напряжений имеет вид:
| (4.2) |
где 
– собственная проводимость узла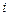 
.
– взаимная проводимость ветви, соединяющей узлы 
.
Собственная проводимость узла равна сумме проводимостей ветвей, сходящихся в данном узле.
Взаимная проводимость равна сумме проводимостей ветвей, соединяющих данные узлы.
Выражение, стоящее в правой части уравнений системы, называют «узловой ток».
Узловой ток (теоретическое понятие) – это алгебраическая сумма произведений 
и 
источника тока (если они есть) всех ветвей, примыкающих к рассматриваемому узлу. Слагаемое входит в выражение со знаком «+», если Э.Д.С. и источник тока направлены к узлу. В противном случае – ставится знак «–».
Из системы (4.2) видно, что собственные проводимости входят в уравнения со знаком «+», а взаимные проводимости – со знаком «–».
Алгоритм расчета электрических цепей по методу узловых напряжений:
1) Выбираем базисный узел. Желательно нулевой потенциал присвоить тому узлу, где сходится большее количество ветвей.
Запомнить! Если в составе цепи имеется одна или несколько ветвей, содержащих идеальные Э.Д.С. (сопротивление таких ветвей равно нулю), то за базисный принимают один из узлов, между которыми находится ветвь с идеальной Э.Д.С.
2) Составляется система уравнений для неизвестных узловых напряжений в соответствии с общей структурой этих уравнений (4.2).
3) Решая данную систему, находят напряжения узлов относительно базиса.
4) Токи ветвей определяют по обобщенному закону Ома:
.
Частным случаем метода узловых напряжений является метод двух узлов. Если схема содержит только два узла, то в соответствие с методом узловых напряжений (в отсутствие идеальных Э.Д.С.) составляется только одно уравнение:
 .
|
Примеры расчета линейных электрических цепей методом узловых напряжений
Пример 4.1
Рис. 4.1
| Дано:
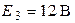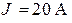 ;  ;  ;  ;    ;  Определить все токи в схеме рис. 4.1 методом узловых напряжений.
|
Решение
Цепь содержит три узла, ветви с идеальными Э.Д.С. отсутствуют. Число необходимых уравнений, определяемое по формуле (4.1), равно двум. В качестве базисного выбираем третий узел.
Система уравнений имеет вид:
,
где
;
;
;
;
.
В результате решения определяем:
;
.
Токи ветвей определяем по обобщенному закону Ома:
;
;
;
;
.
Правильность решения задачи целесообразно проверить составлением и расчетом баланса мощностей.
Уравнение баланса мощностей:
;
;
.
Мощность приемников равна мощности потребителей, т.е. баланс мощностей выполняется.
Проверим выполнение второго закона Кирхгофа для внешнего контура.
Второй закон Кирхгофа:
;
;
.
Ответ: 
, 
, 
, 
, 
.
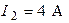Пример 4.2
| Дано:
 ;  ;  ;  ;  ;  ;
 ;
 ;  .
|
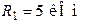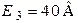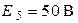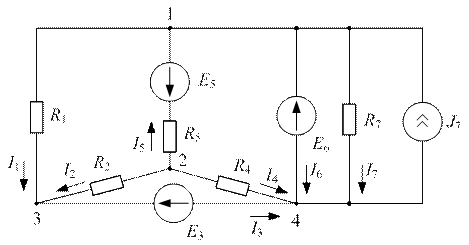
| Рис. 4.2 |
Определить токи в схеме рис. 4.2 методом узловых напряжений.
Решение
В схеме 4 узла. В ветвях 3 и 6 включены идеальные источники Э.Д.С., эти ветви соединяются в узле 4. По формуле (4.1) определяем число уравнений: 
.
Действительно, если за базисный узел принять узел 4 (но также можно принять узел 1 или 3), то сразу определяем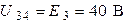 
и 
. Неизвестным является узловое напряжение 
.
Уравнение по методу узловых напряжений имеет вид:
.
где
;
;
;
;
;
.
Определяем токи 
, 
, 
, 
, 
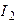по закону Ома:
; 
;
; 
; 
.
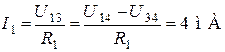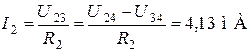Токи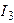 
и 
определяем по первому закону Кирхгофа:
;
.
Ответ: 
, 
, 
, 
, 
, 
.
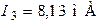Пример 4.3
| Дано:
 ;
 ;
 ;
 ;  ;  .
|
| Рис. 4.3 |
Решение
Особенностью схемы является наличие двух ветвей с идеальными источниками Э.Д.С., которые расположены в ветвях, не имеющих общего узла. В этом случае цепь подвергается следующему преобразованию. В одной из ветвей, содержащих идеальный источник Э.Д.С. (например ветвь с 
), включают компенсирующую Э.Д.С. 
, равную по величине и противоположную по направлению. Точно такая же Э.Д.С. 
включается во все соседние ветви, сходящиеся в одном из узлов данной ветви. Направления включаемых Э.Д.С. по отношению к этому узлу сохраняется (рис. 4.4). Токораспределение в цепи не изменяется.
|
| Рис. 4.4 |
Рисунки 4.5 а, б, в – демонстрируют это преобразование.
Теперь схема (рис. 4.5 в) содержит только одну ветвь с идеальным источником Э.Д.С. 
. Потенциалы узлов 1 и 2 равны, т.к. их соединяет короткозамкнутый участок (рис. 4.5 а). Следовательно ветвь с 
можно удалить из схемы. Примем узел 4 за базисный, тогда
.
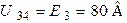Уравнение по методу узловых напряжений имеет вид:
,
где
; 
; 
;
; 
; 
.
|
а
|
б
|
| в |
| Рис. 4.5 |
Переходим к исходной схеме (рис. 4.3). Запишем уравнение по 1–ому закону Кирхгофа для узла 3:
,
откуда
.
Запишем уравнение по 1–му закону Кирхгофа для узла 4:
,
откуда
.
Ток в ветви 5 определим по закону Ома:
.
Ток в ветви с идеальной Э.Д.С.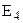 
определим по 1–му закону Кирхгофа:
.
Ответ: 
, , 
, 
, .
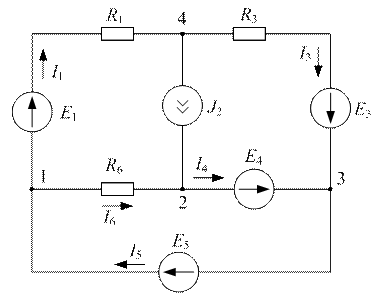
Пример 4.4
|
Дано:
 ;  ;  ;  ;  ;  .
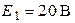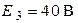Определить токи в схеме рис. 4.6 методом узловых напряжений.
|
| Рис. 4.6 |
Решение
За базисный узел в данной схеме можно принимать 1–ый, 2–ой или 3–ий узлы. Рассмотрим решение задачи в случае, если за базисный принят потенциал 3–го узла. Тогда:
.
Поскольку узлы 1 и 2 связаны с 3–им узлом ветвями, содержащими только идеальные источники Э.Д.С., то:
;
.
Остаётся определить потенциал 4–го относительно 3–го базисного. Составляем одно уравнение:
,
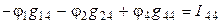где
– взаимная проводимость между 1 и 4 узлами;
– взаимная проводимость между 2 и 4 узлами;
– собственная проводимость 4 узла.
Решаем уравнение:
,
откуда:
.
На основании обобщённого закона Ома для участка цепи, определяем токи:
,
откуда
;
;
;
;
.
Токи в четвёртой и пятой ветвях определим по 1–му закону Кирхгофа:
;
.
Ответ: 
, 
, 
, 
, 
.
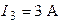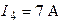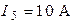Пример 4.5
|
Дано:
 
Определить токи в схеме рис. 4.7 методом двух узлов.
|
| Рис 4.7 |
Решение
За базисный принимаем второй узел: 
Записываем формулу по методу двух узлов:
где
– узловой ток первого узла;
– собственная проводимость первого узла.
Тогда
;
.
Внимание! В собственной проводимости первого узла отсутствует слагаемое 
, так как ветвь, содержащая идеальный источник тока, имеет бесконечно большое сопротивление, а значит её проводимость будет стремиться к нулю.
Определим напряжение 
:
Используя обобщенный закон Ома для участка цепи запишем:
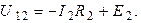
Следовательно, токи в цепи определяются по следующим формулам:
Ответ: 
