Для анализа линейных электрических цепей в установившемся синусоидальном режиме широко используется метод комплексных амплитуд (символический метод). В этом методе оперируют не реальными гармоническими напряжениями и токами, а их комплексными амплитудами:
(3.1)
или комплексными напряжениями и токами:
, (3.2)
где 
– амплитуды напряжения и тока;
U, I – действующие значения напряжения и тока;
– начальные фазы напряжения и тока.
В символическом методе комплексные сопротивления элементов R, L, С равны соответственно
(3.3)
Комплексное сопротивление Z линейного пассивного двухполюсника (рис.3.1,а) в общем случае содержит активную и реактивную составляющие:
(3.4)
где 
– полное сопротивление (модуль Z);
– угол сдвига фаз между напряжением и током двухполюсника (аргумент Z).
Комплексная проводимость Y пассивного двухполюсника, обратная комплексному сопротивлению Z:
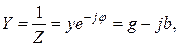(3.5)
где 
– полная проводимость (модуль Y);
Рис.3.1
g – активная проводимость;
b – реактивная проводимость.
Выражению (3.4) соответствует последовательная схема замещения двухполюсника (рис. 3.1,б), а выражению (3.5) – параллельная (рис. 3.1,в). Переход от последовательной схемы замещения к параллельной осуществляют по формулам
(3.6)
Для обратного перехода используют выражения
(3.7)
 |  | ||
Для расчетов токов и напряжений в цепях с единственным источником энергии применяют метод эквивалентных преобразований (МЭП). Например, для цепи на рис.3.2 две параллельные ветви с комплексными сопротивлениями
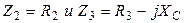заменяют одной эквивалентной ветвью с сопротивлением
Рис.3.2 Рис.3.3
Тогда входное комплексное сопротивление цепи равно
Вычислив входной ток
токи 
целесообразно рассчитать, используя «правило плеч»;
(3.8)
Расчет токов и напряжений завершается построением топографической диаграммы (рис.3.3). Построение диаграммы следует производить, взяв в качестве исходной точки «отрицательный» зажим источника, т.е. узел 4. Двигаясь против токов ветвей, строят на диаграмме векторы комплексных напряжений всех элементов цепи. Координаты точек 3, 2, 1 равны значениям комплексных потенциалов соответствующих узлов цепи (предполагается 
). Особенность диаграммы: вектор напряжения 
между любой парой узлов m и n направлен на диаграмме от узла n к узлу m. Для расчета цепи на рис.3.2, а также более сложных цепей лестничной структуры применяется метод пропорционального пересчета (МПП). В этом методе используется свойство линейной зависимости всех токов и напряжений цепи от амплитуды напряжения (тока) источника (в цепи единственный источник). Поясним суть метода для цепи на рис.3.2. Задается условно значение тока в наиболее удаленной и сложной ветви цепи. Пусть, например, 
. Затем, находя условное напряжение 
и условный ток 
сложив токи 
, находят ток 
.
Тогда
Разделив истинное напряжение 
на условное 
вычисляют комплексный коэффициент пересчета К:
Для получения истинных напряжений и токов цепи необходимо все найденные ранее условные напряжения и токи умножить на коэффициент К, т.е.
Для ориентировочных расчетов напряжений и токов применяется также графоаналитический метод расчета. Этот метод методологически связан с методом пропорционального пересчета, однако не использует алгебры комплексных чисел. Пусть, как и в предыдущем методе, 
Выбрав масштабы 
и 
для напряжений и токов, откладывают в произвольном направлении ток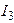 
(например горизонтально). Затем строят вектор напряжения 
совпадающий по направлению с током 
,и вектор напряжения 
отстающий по фазе от на 90°. Используя графические измерения, вычисляют напряжение 
Вычислив 
и откладывая ток 
параллельно 
графически определяют 
и т.д. В результате находят вектор условного напряжения U. Затем с помощью коэффициента пересчета K=U/U' вычисляют истинные токи и напряжения. Графические построения по ходу расчета дают в итоге условную топографическую диаграмму. Для получения истинной диаграммы следует, во-первых, увеличить линейные размеры всех векторов в К раз, во-вторых, повернуть против часовой стрелки условную диаграмму на угол 
, равный разности начальных фаз векторов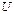 
и. 
Активная и реактивная мощности потребителей вычисляются по формулам
Комплексная мощность источника находится из
где – комплексное напряжение источника;
– сопряженный комплексный ток источника.
Из закона сохранения энергии вытекают условия баланса активных и реактивных мощностей:
Описание лабораторной установки
В состав лабораторной установки входят перестраиваемый генератор синусоидального напряжения, вольтметр, фазометр и лабораторный макет. На макете смонтированы три резистора 
конденсатор и катушка индуктивности. Для подключения генератора на макете имеется дополнительная пара зажимов.
Генератор. При установке частоты генератора следует ручку множителя частоты переключить в нужное положение и, вращая лимб генератора, установить требуемую частоту. Напряжение генератора устанавливается вращением ручки «Регулировка выхода».
Измерение напряжения генератора производится только внешним вольтметром, вольтметр, встроенный в генератор, в лабораторных работах не используется.
Вольтметр. В общем случае перед включением вольтметра переключатель пределов следует установить на предел 30 В и при небольших отклонениях стрелки прибора переходить на более низкие пределы. Цена деления вольтметра зависит от положения переключателя пределов и определяется как частное от деления установленного предела на число делений шкалы.
Фазометр. Фазометр позволяет измерить угол сдвига фаз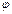 
между двумя напряжениями одинаковой частоты, называемыми «Сигнал» и «Опорное», причем показание фазометра равно углу фазового сдвига напряжения «Сигнал» по отношению к опорному напряжению, т.е.
.
Фазометром можно измерить непосредственно угол сдвига фаз напряжений ветвей (элементов), имеющих общий узел. К общему узлу подключается зажим «Земля» фазометра. К двум оставшимся узлам подключаются клеммы «Опорное» и «Сигнал» фазометра, причем не принципиально, какое из напряжений принять в качестве опорного. Однако нужно следить, чтобы напряжения «Опорное» и «Сигнал» были направлены к общему узлу (напряжения 
и 
на рис.3.4,а).
Из рис.3.4,б следует, что переход от напряжений 
к обратным им напряжениям 
не изменяет фазового угла 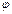между ними как по величине, так и по знаку. Из сказанного ясно, что в качестве напряжений «Сигнал» и «Опорное» можно принять не только напряжения 
, направленные к зажиму «Земля», но в равной мере и обратные им напряжения 
направленные от зажима «Земля». Назовем напряжения «Сигнал» и «Опорное» согласованными (по отношению к зажиму «Земля»), если они оба направлены к зажиму «Земля» или оба от зажима «Земля». Таким образом, показание фазометра на рис.3.4,а равно углу 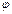сдвига фаз между напряжением «Сигнал» и согласованным с ним напряжением «Опорное». Если же нас интересует угол а фазового сдвига между несогласованными напряжениями «Сигнал» и «Опорное», то из рис.3.4,б следует, что в этом случае к показанию фазометра 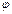следует добавить или вычесть 180°, причем выбор знака для слагаемого 180° определяется только удобством представления угла а.
Рис. 3.4.
Обобщая все сказанное выше, можно для рис.3.4,а записать
(3.11)
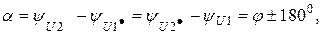(3.12)
где 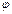показание фазометра;
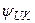начальная фаза напряжения 
.
Если начальная фаза опорного напряжения равна нулю, то из (3.10) видно, что в этом случае фазометр регистрирует начальную фазу напряжения «Сигнал».
Фазометр может применяться для измерения начальных фаз токов ветвей, однако в этом случае напряжение «Сигнал» должно сниматься с резистивного элемента ветви, фаза напряжения в котором совпадает с фазой тока.
В табл.3.1 заданы для шести вариантов параметры генератора 
и номиналы элементов исследуемых схем. Величины 
и 
задают резистивное сопротивление и индуктивность для последовательной схемы замещения реальной катушки индуктивности. Конденсатор заменяется идеальной емкостью С.
Домашнее задание
1. Для последовательной цепи на рис.З.5:
а) рассчитать согласно варианту сопротивления 
реактивных элементов, комплексное входное сопротивление цепи, комплексный ток f и комплексные напряжения элементов 
Параметры цепи и генератора заданы в табл.3.1 согласно варианту. Напряжение генераторе У=10 В. Начальную фазу напряжения генератора принять нулевой. Расчетные комплексные величины занести в табл.3.2 в графу «Расчет»;
б) по результатам расчетов построить топографическую диаграмму напряжений всех элементов с указанием вектора тока.
2. Для параллельной цепи на рис.3.6 и указанных в 
a параметров генератора:
а) рассчитать по закону Ома комплексные токи 
ветвей и входной ток 
как их сумму. Результаты занести в табл.3.3 в графу «Расчет»;
6) построить векторную диаграмму токов и напряжений.
Таблица 3.1
| 200. Вариант 201. | 202. Схема на рис. 203. | 204.
| 205. 
| 206.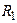 
| 207.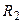 
| 208. 
| 209.
| 210.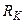 
| 211. 
|
| 212. В 213. | 214. Гц 215. | 216. Ом 217. | 218. Ом 219. | 220. Ом 221. | 222. мГн 223. | 224. Ом 225. | 226. мкФ 227. | ||
| 228. 1 229. | 230. 3.8 231. | 232. 10 233. | 234. 700 235. | 236. 139 | 237. 139 238. | 239. 139 240. | 241. 44 242. | 243. 58 244. | 245. 0.93 246. |
| 247. 2 | 248. 3.8 249. | 250. 10 251. | 252. 1200 253. | 254. 139 255. | 256. 139 257. | 258. 139 259. | 260. 42 261. | 262. 60 263. | 264. 0.93 265. |
| 266. 3 267. | 268. 3.9 269. | 270. 10 271. | 272. 1300 273. | 274. 143 275. | 276. 143 277. | 278. 143 279. | 280. 42 281. | 282. 56 283. | 284. 0.95 285. |
| 286. 4 287. | 288. 3.9 289. | 290. 10 291. | 292. 800 293. | 294. 143 295. | 296. 143 297. | 298. 143 299. | 300. 42.5 301. | 302. 56 303. | 304. 0.99 305. |
| 306. 5 307. | 308. 3.10 309. | 310. 10 311. | 312. 1000 313. | 314. 157 315. | 316. 137 317. | 318. 157 319. | 320. 44 321. | 322. 57 323. | 324. 0.96 325. |
| 326. 6 327. | 328. 3.10 329. | 330. 10 331. | 332. 500 333. | 334. 142 335. | 336. 142 337. | 338. 142 339. | 340. 45 341. | 342. 57 343. | 344. 1.0 345. |
3. В разветвленной цепи, заданной согласно варианту в табл.3.1:
а) рассчитать, используя метод эквивалентных преобразований, комплексные токи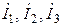 
ветвей и комплексные напряжения всех элементов. Результат занести в табл.3.4 в графу «Расчет» (
– напряжения на резисторах 
);
б) построить топографическую диаграмму напряжений всех элементов и совмещенную с ней векторную диаграмму токов. Для векторов напряжений и векторов токов желательно цветовое различие, масштабы для 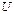и взять достаточно крупными;
в) составить и рассчитать уравнения баланса активных и реактивных мощностей цепи. Вычислить коэффициент мощности цепи.
