Электрический ток и напряжение, изменяющиеся во времени по какому–либо закону, называют переменными.
Если форма кривой переменного тока и напряжения повторяется через равные промежутки времени, то их называют периодическими.
Наименьшее время, через которое повторяется форма переменного тока и напряжения, называют периодом, обозначают 
и измеряют в секундах.
Число периодов в 1 секунду называют частотой 
переменного тока и напряжения, размерность частоты в единицах СИ: 1 Герц [Гц].
.
Простейшими периодическими переменными током и напряжением являются вырабатываемые генераторами всех видов электростанций напряжение и токи синусоидальной формы:
Напряжение:
,
,
где:
, 
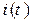– мгновенные значения тока и напряжения;
, 
– амплитудные значения тока и напряжения;
, 
– начальные фазы тока и напряжения;
– угловая частота, (единица измерения 
).
Разницу начальных фаз напряжения и тока обозначили 
и назвали углом сдвига фаз.
Для расчёта цепей синусоидального тока применяется метод комплексных амплитуд (символический метод расчёта), основанный на использованиитеории комплексных чисел.
| Из курса «Высшая математика» известно, что комплексное число можно представить в виде вектора на комплексной плоскости, а действительная и мнимая части комплексного числа есть проекции вектора на вещественную и мнимую оси (рис. 6.1). |
| Рис 6.1 |
(В теории электрических цепей буква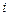 
обозначает ток, поэтому за признак мнимости принята буква 
(
), а само комплексное число обозначается или точкой поверх буквы или подчёркиванием буквы снизу: 
, 
): 
, 
,
где 
– модуль; 
– аргумент или фаза комплексного числа.
Синусоидальная функция условно представляется вектором, длина которого определяется максимальным или действующим его значением, а направление – её начальной фазой. Положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов (против часовой стрелки).
Синусоидальный ток в однородных идеальных элементах: резисторе, индуктивности, ёмкости. Временные и векторные диаграммы.
а) Синусоидальный ток в активном сопротивлении
| 
|
|
|
б) Синусоидальный ток в индуктивности
| 
|
|
|
в) Синусоидальный ток в ёмкости
| 
|
|
|
Если 
, то комплекс амплитудного и действующего значений запишется соответственно: 
, 
.
Если задан комплекс действующего значения напряжения 
, то его мгновенное значение имеет вид: 
.
