Следовательно, полное комплексное сопротивление равно резистивному сопротивлению: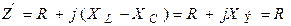 
. Ток при резонансе 
– максимален.
Условие возникновения резонанса напряжений в контуре (рис. 7.1):
.
Резонансная частота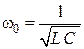 
или 
.
Из векторной диаграммы контура в режиме резонанса (рис. 7.2) следует, что входное напряжение равно напряжению на активном сопротивлении.
|
| Рис. 7.2 |
Характеристическое сопротивление, добротность, затухание контура
Резонансная частота (
); характеристическое сопротивление (
) и добротность (
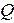) являются вторичными параметрами контура.
а) Характеристическое сопротивление – это сопротивление индуктивности и ёмкости при резонансе:
.
б) Добротность – это отношение максимальной энергии электрического и магнитного полей (
) к потерям в контуре (
)или отношение действующих значений напряжений на реактивных элементах к приложенному напряжению в режиме резонанса:
.
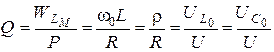Добротность характеризует качество контура и определяет его резонансные свойства. В реальных устройствах к сопротивлению 
надо прибавить 
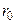источника, что снижает результирующую добротность.
в) Затухание – величина, обратная добротности:
.
г) Полоса частот вблизи резонанса, на границах которой ток снижается до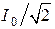 
от максимального значения 
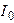тока при резонансе, определяет абсолютную полосу пропускания контура (рис. 7.3):
,
где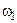 
и 
граничные частоты полосы пропускания.
Зная ширину полосы пропускания, можно определить добротность контура:
.
|
| Рис. 7.3 |
Рассмотрим, как определить резонансную частоту колебательного контура рис. 7.4
Рис. 7.4
Особенностью цепи является наличие шунта 
, подключенного параллельно к емкости, который изменяет сопротивление цепи.
Резонансную частоту определим из условия равенства нулю эквивалентного реактивного сопротивления контура. Запишем полное комплексное сопротивление цепи, выделим действительную и мнимую части:
.
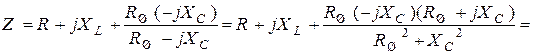
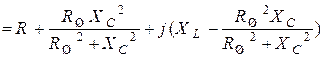В режиме резонанса 
(полное сопротивление носит активный характер), следовательно:
или 
,
откуда 
.
Векторная диаграмма колебательного контура (рис. 7.4) в режиме резонанса представлена на рис. 7.5.
|
| Рис. 7.5 |
Напряжение на входе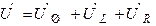 
.
На диаграмме видно, что входное напряжение 
совпадает по фазе с током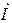 
, что соответствует условию режима резонанса. 
Параллельный колебательный контур. Резонанс токов
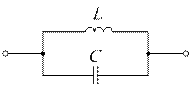
Эквивалентные схемы параллельных колебательных контуров представлены на рис. 7.6 а – в.
| 
|
|
| Рис. 7.6. а | Рис. 7.6. б | Рис. 7.6. в |
Явление резонанса в схеме образованной двумя параллельными ветвями с разнохарактерными сопротивлениями, называется резонансом токов. Условием резонанса токов является равенство нулю реактивной части полной комплексной проводимости параллельного колебательного контура.
Проводимости ветвей схемы рис. 7.6. в) равны:
;
,
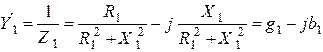где 
, 
.
.
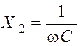Т.к. при резонансе 
, то полная проводимость должна носить активный характер, что возможно при 
, т.е.
.
Решив это равенство относительно резонансной частоты 
, получим:
.
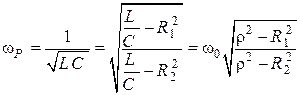В частном случае идеального контура (рис. 7.6. а) 
.
Полная проводимость идеального контура 
, следовательно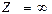 
. Таким образом, идеальный контур при резонансе токов эквивалентен разрыву цепи.
