Основные теоретические положения. Закон Ома
Участок ветви, содержащий один или несколько источников энергии, является активным. Рассмотрим участок электрической цепи (рис. 1.1).
|
| Рис. 1.1 |
При решении задач по теории электрических цепей выбирают положительное направление тока, которое указывается стрелкой.
Направление тока характеризуется знаком тока. Понятия положительный или отрицательный участок имеют смысл, если сравнивать направление тока в проводнике с некоторым заранее выбранным направлением – так называемым положительным направлением тока.
Запомнить!
1) Ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е потенциал падает по направлению тока (на рис. 1.1 условно точке «а» присвоим знак «+», а точке «с» – знак «–»).
2) Э.Д.С., направленная от точки «c» к точке «d», повышает потенциал последней на величину 
(на рис. 1.1 условно зажиму Э.Д.С., подключенному к точке «c», присвоим знак «–», а зажиму, подключенному к точке «d» – знак «+»).
3) Напряжение 
положительно, когда потенциал точки «a» выше, чем потенциал точки «c».
При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она направляется от точки высшего потенциала к точке низшего потенциала.
На рис. 1.1 ток протекает от точки «a» к точке «c», значит, потенциал 
будет меньше 
на величину падения напряжения на сопротивлении 
, которое по закону Ома равно 
: 
.
На участке «c - d» Э.Д.С. 
действует в сторону повышения потенциала, следовательно, 
.
Потенциал точки «b» равен:
.
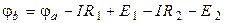Знак «–» перед Э.Д.С., совпадающей по направлению с током, объясняется следующим образом: напряжение на участке с Э.Д.С. противоположно направлено самой Э.Д.С. и определяемому напряжению.
Напряжение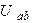 
найдем как разность потенциалов:
 .
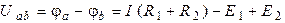| (1.1) |
Ток на участке ab определяют по выражению
 .
| (1.2) |
Формула (1.2) выражает обобщенный закон Ома, или закон Ома для активного участка цепи.
Из формулы видно, что если ток, напряжение и Э.Д.С. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если Э.Д.С. действует в сторону, противоположную положительному направлению тока, в выражении ставится знак «–».
Закон Ома применяется как для участка ветви, так и для одноконтурной замкнутой схемы.
Законы Кирхгофа
Для расчета разветвленных электрических цепей применяют 1–ый и 2–ой законы Кирхгофа. Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.
Законы Кирхгофа наряду с законами Ома являются основными в теории электрических цепей.
Первый закон Кирхгофа:
Алгебраическая сумма токов в узле равна нулю:
 ,
| (1.3) |
где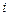 
– число ветвей, сходящихся в данном узле, т.е. суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.
Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:
,
где 
– число узлов в рассматриваемой цепи.
Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.
Уравнения, составленные по первому закону Кирхгофа, называются узловыми.
Второй закон Кирхгофа:
Алгебраическая сумма Э.Д.С. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:
 ,
| (1.4) |
где 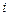– номер элемента (сопротивления или источника напряжения) в рассматриваемом контуре.
Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:
,
где 
– число ветвей электрической цепи, – число узлов, 
– число источников тока.
|
| Рис. 1.2 Иллюстрация ко второму закону Кирхгофа |
Для того чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнить следующие действия:
1) Произвольно выбрать направление обхода контура, например, по часовой стрелке.
2) Э.Д.С. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если Э.Д.С. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «–».
С учетом вышеперечисленного второй закон Кирхгофа для схемы рис.1.2 запишется следующим образом:
,
или
.
Уравнения, составленные по второму закону Кирхгофа, называются контурными.
