Вопрос1 Классическая механика и границы ее применимости. Материальная точка. Система отсчета. Кинематические уравнения
Классическую механику подразделяют на кинематику, статику и динамику.
Материальная точка- тело, размерами которого можно пренебречь. Движение материальной точки по отношению к системе отсчета может быть задано векторным или координатным способами.
При векторном способе положение точки А, рис. 1, в момент времени t определяется ее радиусом вектором 
, проведенным из начала координат до движущейся точки.
Закон движения дается векторным уравнением 
. При координатном способе положение точки А определяется координатами x, y, z, а закон движения задается тремя уравнениями:
при этом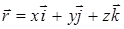 
Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом.
Вопрос 2 Траектория, путь, перемещение. Средняя и мгновенная скорости. Равномерное прямолинейное движение
Непрерывная линия, которую описывает точка при своем движении, называется траекторией. Путь – это длина траектории, пройденная точкой.
Перемещение- изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения
Мгновенная скорость 
Средняя скорость Vср=S/t
Вопрос 3 Ускорение. Нормальная и тангенциальная составляющие ускорения. Равнопеременное движение
Ускорение- быстрота изменения скорости
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости 
Нормальное ускорение возникает всегда при движении точки по траектории с ненулевой кривизной. Характеризует изменение скорости по направлению.
= 
Равнопеременное движение — движение с постоянным ускорением.
V(t)=V0+at
x(t)=x0+V0t+at 
/2
Вопрос 
4 Движение материальной точки по окружности. Угол поворота, угловая скорость, угловое ускорение
Рассмотрим движение материальной точки по окружности радиуса R Пусть за время 
точка повернется на угол 
, тогда угловая скорость
,
Угловое ускорение характеризует быстроту изменения угловой скорости, т.е.
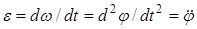
Вопрос 5. Связь между линейными и угловыми кинематическими характеристиками
Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.
При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь
s = rφ. (1)
За малое время Δ t точка проходит расстояние Δ s = rφ 2− rφ 1, где φ 2 и φ 1 — углы поворота в конце и в начале интервала Δ t. Разделив последнее равенство на Δ t и учитывая, что Δ s Δ t = υ и φ 2− φ 1Δ t =Δ φ Δ t = ω, получим
υ = rω. (2)
Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δ t есть Δ υ = rω 2− rω 1, где ω 2 и ω 1 — угловые скорости в конце и в начале промежутка Δ t. Разделим последнее равенство на Δ t и учтем, что Δ υ Δ t = ak и ω 2− ω 1Δ t =Δ ω Δ t = ε, тогда касательное ускорение
ak = rε. (3)
Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.
Доп. Инф
При движении точки по кривой линейная скорость направлена по касательной к кривой и по модулю равна произведению угловой скорости на радиус кривизны кривой.
