6.1. Пусть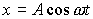 
и 
, тогда траекторией будет прямая линия, рис. 5: 
.
6.2. Пр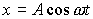и и 
, траекторией будет эллипс, (рис. 6):
(x2/A2)+(y2/B2)=1.
При разных частотах складывающихся колебаний результирующие траектории будут иметь более сложный вид.
Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу.
Математический маятник
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся наневесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения[1]. Период малых собственных колебанийматематического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит[2] от амплитуды колебаний и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где 
― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция 
― это угол отклонения маятника в момент 
от нижнего положения равновесия, выраженный в радианах; 
, где 
― длина подвеса, 
― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:
.
Вопрос 50 Физический маятник
|
.
Решением его будет 
.
Период колебания 
, (15)
где L = J/ml - приведенная длина физического маятника; L - это длина такого математического маятника, период колебаний которого совпадает с периодом колебания данного физического маятника.
Дифференциальное уравнение свободных затухающих колебаний (механических) и его решение.
Автоколебания.
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.
Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяется. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями.
Дифференциальное уравнение свободных затухающих колебаний линейной системы
где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде 
(7.1) где u=u(t).
После нахождения первой и второй производных и их подстановки в (1) получим
Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен: 
(7.2)
Тогда получим уравнение решением которого является функция u=A0cos(ωt+φ). Значит, решение уравнения (7.1) в случае малых затуханий
