Параллельным колебательным контуром называется электрическая цепь, в которой индуктивности и емкости распределены по двум параллельным ветвям, подключенным параллельно к источнику энергии. Принципиальные схемы контуров любого вида можно заменить схемами замещения двух видов (показаны на рис. 28 а и б).
  а). б).
а). б).
|
Рис. 28 – Схемы параллельных колебательных контуров
Рассмотрим схему, представленную на рис. 28б. Комплексная функция входного сопротивления для нее:
| Zвх(jω)= (R + jωL)(1/jωС) / [R + jωL+ 1/(jωC)]. | (23) |
На частотах, близких к резонансной (ω ≈ ωо ), и больших добротностях контура (Q >>1) справедливо неравенство R<<ω0L.
Тогда с учетом (17)-(18) комплексная функция входного сопротивления
| Zвх(jω) = R0e /(1+jξ). | (24) |
На частоте резонанса входное сопротивление параллельного резонансного контура имеет чисто резистивный характер. Резонансное сопротивление параллельного контура R0e в Q2 раз превышает сопротивление потерь последовательного колебательного контура:
| R0e = L/(RC) = ρ2/R = ρQ = RQ2. | (25) |
Частотная характеристика полного входного сопротивления
| Zвх(ω) = R0e / √(1+ξ2), | (26) |
а фазо-частотная характеристика
| φ(ω) = – arctg ξ. | (27) |
Резонанс в параллельном контуре наблюдается на частоте, при которой реактивная составляющая входного сопротивления равна нулю и комплексное сопротивление вещественно. В (24) это будет при ξ =0, т.е. на резонансной частоте последовательного контура (16). Выражение (24) верно при R<<ω0L. Более точное выражение для резонансной частоты можно получить, приравнивая нулю правую часть (23):
| ω0п = ω0 √ 1 – 1/Q2. | (27) |
Из (27) следует, что резонансная частота параллельного контура при учете сопротивления потерь меньше резонансной частоты последовательного контура.
Передаточная функция параллельного контура по току равна
| КI (jω) = ỈC / Ỉ1 = jωCZвх(ω) = j Q ω /[ω0(1 + jξ)]. | (28) |
Т. к. ŮC = Ů1, передаточная функция по напряжению КU (jω)=1. В параллельном колебательном контуре на резонансной частоте ток в контуре IС в Q раз больше входного тока (т.е. в параллельном контуре наблюдается резонанс токов).
Задание. Собрать схему, представленную на рис. 29. Изменяя значения R, С и L, снять амплитудно-частотные и фазо-частотные характеристики параллельного контура. Изучить влияние параметров контура на его характеристики – резонансную частоту, добротность, полосу частот.
Порядок выполнения.
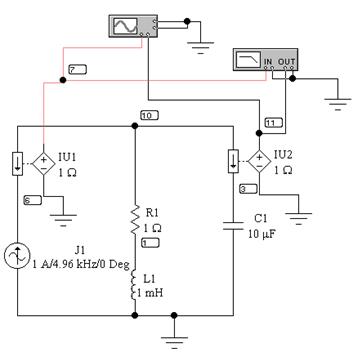
Как отмечалось выше, в параллельном колебательном контуре наблюдается резонанс токов, поэтому на контур подается сигнал с источника тока J1(коэффициент передачи по напряжению равен 1). Для измерения токов можно воспользоваться источниками напряжения, управляемыми током (IU1 и IU2 на рис. 29). Напряжение на выходе этих элементов пропорционально токам, протекающих в первичной цепи этих источников. Коэффициент передачи этих источников равен отношению выходного напряжения к току в первичной цепи и имеет размерность Ом. В данном примере этот коэффициент равен 1В/1А=1 Ом. Таким образом, сигналы, подаваемые на вход измерительных приборов (осциллографа и плоттера), будут пропорциональны токам, протекающим во входной цепи и через емкость соответственно.
На плоттере удобно наблюдать и измерять АЧХ и ФЧХ. С помощью осциллографа можно наблюдать соотношение между входным и выходным сигналом (сигналы пропорциональны токам!). Для этих исследований необходимо изменять частоту источника тока J1.
|
Рис. 29 – Схема измерения параметров параллельного колебательного контура
Способы измерения с помощью опций меню Analysis и измерителя АЧХ и ФЧХ подробно изложены в работе 6.
Используя описанные методики, измерить и занести в таблицу 13 параметры амплитудно-частотной и фазо-частотной характеристик параллельного контура для следующих значений элементов:
А). R=0,1 Ом, С=1 мкФ и L=1, 2 …..10 мГн;
Б). R=0,1 Ом, L= 1 мГн и С=1, 2……10 мкФ;
В).L= 1 мГн, С=1 мкФ и R =1, 2 …….10 Ом.
По результатам измерений построить амплитудно-частотные и фазо-частотные характеристики, а также годографы комплексной передаточной функции параллельного резонансного контура.
Построить зависимости характеристик контура – резонансной частоты, добротности, полосы частот – от значений R, L и C.
Табл.13
| f1,Гц | f2,Гц | fn,Гц | ωo | Q | |||
| R=….. L=….. C=….. | Кu | ||||||
| φ,град |
Контрольные вопросы:
1. Как определяются токи в цепи синусоидального тока с параллельным соединением резистора, индуктивности и ёмкости. Запишите закон Ома в комплексной форме.
2. Что такое треугольник проводимостей? Как его построить?
3. Какую цепь называют параллельным колебательным контуром?
4. При каком условии в параллельном колебательном контуре наступает резонанс? Почему резонанс в такой цепи называют резонансом токов?
5. Как определяется резонансная частота?
6. Что называют характеристическим сопротивлением контура и добротностью контура?
7. Изменением каких величин в параллельном колебательном контуре можно достичь резонанса токов?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 8
«ИССЛЕДОВАНИЕ СВЯЗАННЫХ КОНТУРОВ»
Цель: изучить основные виды связи и их влияние на свойства, временные и частотные характеристики связанных контуров.






