Исходные данные для расчетов

1. Прямоугольный: а) четный; б) нечетный импульсы.

2. Треугольный импульс.

3. Косинусоидальный и синусоидальный импульсы:

a) s(t) = E cos w_ot; б) s(t) = E sin w_ot.

4. Экспоненциальный импульс: s(t) = U exp (-at).

 

Варианты/ Параметры
Амплитуда, В
Длительность импульса, мс	0,01	0,1
a, с-1	0,1	0,2	0,3	0,4	0,5	0,6	0,7

 

Контрольные вопросы:

1. Как можно определить физический смысл спектральной плотности?

2. Какими характерными особенностями отличаются спектральные плотности для сигналов, являющихся четными функциями времени?

3. Какими функциями частоты являются действительная и мнимая части спектральной плотности?

4. В чем принципиальное отличие амплитудных и фазовых спектров периодических и непериодических сигналов?

5. Определите значение спектральной плотности сигнала при изменении его масштаба времени с коэффициентом к = – 1 и проанализируйте полученный результат.

6. Какому виду импульсов соответствует свойство смещения спектра сигнала, используемое при умножении его функции на гармоническое колебание?

7. В чем характерная особенность спектра дельта-функции?

8. Какую роль играет фаза спектральной плотности сигнала при определении его энергетического спектра?

9. Могут ли два нетождественных сигнала обладать одним и тем же энергетическим спектром?

 

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 3

«ДЕЛИТЕЛИ НАПРЯЖЕНИЯ И ТОКА»

Цель: изучить правила делителей напряжения и тока и проанализировать предложенные схемы.

Краткие теоретические сведения

Делитель напряжения

На рис. 1 представлена простейшая схема делителя напряжения на двух резисторах R1 и R2. К цепи приложено напряжение источника постоянного тока Е. Через резисторы протекает ток I (последовательное включение), на резисторе R1 падает напряжение U1, на резисторе R2 – напряжение U2:

I= E /(R1 + R2),
U1=I1R1=E R 1/(R1+R2),	(1)
U2=I1R2=E R 2/(R1+R2).

Задание. По формулам (1) рассчитать падение напряжения на резисторах R1 и R2 для данных, приведенных в табл.1. Результаты расчетов занести в таблицу.

Порядок выполнения. Собрать схему делителя, представленную на рис. 1.

Е

Рис. 1 – Схема делителя напряжения

 

Провести экспериментальную проверку полученных результатов. Изменяя в схеме значения сопротивлений и напряжения источника питания, заполните таблицу 1.

Табл.1

V3, В	R1, Ом	R2, Ом	Ток I (мА)	Напряжение U1(В)	Напряжение U2(В)
Расчет	Эксперимент А1	Расчет	Эксперимент V1	Расчет	Эксперимент V2
	Те же значения сопротивлений

 

По результатам измерений построить зависимости U1=f(R1) при R2=const и U2= f(R2) при R1=const для двух значений V3. Сравнить и проанализировать полученные теоретические и экспериментальные результаты.

 

Делитель тока

На рис. 2 представлена простейшая схема из двух параллельно включенных сопротивлений R1 и R2. К ним приложено напряжение источника постоянного тока Е. Через резистор R1 протекает ток I1, через резистор R2 ток I2. Через оба резистора протекает суммарный ток

I = I1 +I2.

В свою очередь

I1 = E/R1, I2 = E/R2
I = E/R1+E/R2 = E (1/R1+1/R2) = E(R1 + R2)/(R1R2)= E/Ro,	(2)
Ro = (R1R2)/(R1+R2).

 

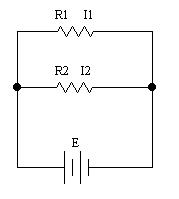
Рис. 2 – Схема делителя тока

 

Задание. По формулам (2) рассчитать токи через резисторы R1 и R2 для данных, приведенных в табл. 2. Результаты расчетов занести в таблицу.

Порядок выполнения. Собрать схему делителя, представленную на рис. 3.

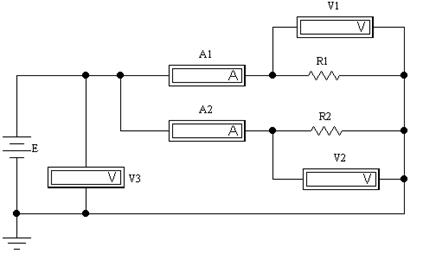
Рис. 3 – Схема параллельной цепи

 

Провести экспериментальную проверку полученных результатов. Изменяя в схеме значения сопротивлений и напряжения источника питания, заполнить таблицу 2.

Табл.2.

V3, В	R1, Ом	R2, Ом	Ток I1 (мА)	Ток I2(мА)	Напряжение эксперимент	Ток I (мА)	RO, Ом
Расчет	Экспери-мент А1	Расчет	Экспери-мент А2	V1	V2
	Те же значения сопротивлений

 

По результатам измерения построить зависимости I=f(Ro) для двух значений V3. Сравнить и проанализировать полученные теоретические и экспериментальные результаты.

 

 

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 4

«ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ RC-ЦЕПЕЙ»

Цель: изучить частотные характеристики RC-цепей, сравнить и проанализировать их для двух предложенных схем.