«ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ»
Цель: Освоение методики проведения анализа непериодических сигналов, расчета их основных характеристик и изучение свойств преобразования Фурье в применении к определению спектральной плотности основных видов непериодических сигналов.
Краткие теоретические сведения. Для выполнения данной работы необходимо знание следующих основных понятий и формул: прямое и обратное преобразования Фурье и их свойства; модуль и аргумент спектральной плотности; амплитудные и фазовые спектры непериодического сигнала и правила их построения; энергия непериодического сигнала и ее распределение в спектре.
Выражения, определяющие взаимосвязь между функцией сигнала и его спектральной функцией, называются парой преобразований Фурье.
 (1)
(1)
 (2)
(2)
Формулы (1) и (2) называются соответственно прямым и обратным преобразованиями Фурье.
Спектральная плотность импульса сигнала обладает всеми свойствами коэффициентов комплексного ряда Фурье. Можно записать:
S(ω) = A(ω) – jB(ω) (3)
 ;
; 
 (4)
(4)
Модуль и аргумент спектральной плотности соответственно являются амплитудно - частотной и фазо - частотной характеристиками импульсного сигнала, и определяются:
 – АЧХ; (5)
– АЧХ; (5)
 – ФЧХ. (6)
– ФЧХ. (6)
В силу своего определения АЧХ является четной функцией частоты, а ФЧХ – нечетной.
Свойства преобразования Фурье:
1. Сдвиг колебания во времени.
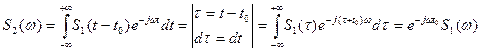 . (7)
. (7)
Сдвиг сигнала по оси времени на произвольную величину t0 приводит к изменению фазовой характеристики спектральной функции на ωt0.
2. Изменение масштаба времени.
 . (8)
. (8)
При сжатии колебания в к раз по оси времени во столько же раз расширяется его спектр по оси частот. Модуль спектральной плотности при этом уменьшается в к раз. Очевидно, что при растяжении сигнала во времени имеет место сужение спектра и увеличение модуля спектральной плотности.
3. Смещение спектра колебания.
 (9)
(9)
Умножение исходного сигнала на гармоническое колебание приводит к расщеплению его спектра на две составляющие, смещенные относительно исходного соответственно на ± w0.
4. Дифференцирование и интегрирование сигналов.
 . (10)
. (10)
Для производной п -го порядка и интеграла данного сигнала соответственно:
 ;
;  .
.
Таким образом, операциям дифференцирования и интегрирования по временной области соответствует операция обычного алгебраического умножения в области частотной. При этом дифференцирующие и интегрирующие цепи можно рассматривать соответственно как обострители и сглаживающие фильтры для исходных сигналов.
5. Сложение и умножение двух колебаний.
Поскольку преобразование Фурье является линейным, то для суммы любого количества сигналов S(t) = S1(t) + S2(t) + S3(t) +... их результирующая спектральная плотность будет определяться соответствующей суммой:
S(ω) = S1(ω) + S2(ω) + S3(ω) +... (11)
Для произведения двух сигналов s(t) = u(t) v(t) результирующая спектральная плотность определится интегралом свертки:
 (12)
(12)
Операция свертки коммутативна, т.е. S(ω) = U(ω)*V(ω) = V(ω)*U(ω).
6. Инверсия аргумента.
Для четных колебаний справедливо следующее правило: если  , то
, то  .
.






