Контур состоит из последовательно соединенных элементов R, L, С. Схема последовательного резонансного контура представлена на рис. 20.
|
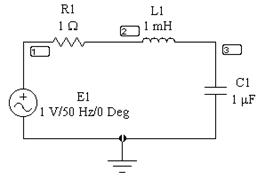
Рис. 20 – Схема последовательного резонансного контура
Комплексная функция входного сопротивления
| Zвх = R + jωL + 1/jωС = R + j[ωL – 1/(ωC)]. | (15) |
При изменении частоты от 0 до ∞ реактивная составляющая сопротивления контура изменяется от –∞ до +∞. На частоте ωо реактивное сопротивление контура равно нулю:
| ωоL – 1/(ωоC) = 0 |
Частота
| ωо = 1 / √ LC | (16) |
называется резонансной частотой. На этой частоте индуктивное сопротивление контура компенсирует емкостное сопротивление, поэтому полное комплексное сопротивление (15) становится равным активной составляющей R. Реактивное сопротивление контура
| X вх = ωL – 1/(ωC) = ρ (ω/ωo – ωo/ω), где ρ = √ LC = ωoL = 1/(ωoC). | (17) |
Величина ρ называется характеристическим сопротивлением контура, которое равно реактивному сопротивлению индуктивности или емкости контура на резонансной частоте.
Подставив (17) в (15) получим
| Zвх = R (1 + jξ), где ξ = Q (ω/ωo – ωo/ω), Q = ρ / R = ωоL / R = 1/(ωоRC). | (18) |
Величина ξ называется обобщенной расстройкой, а величина Q – добротностью резонансного контура, равной отношению характеристического сопротивления контура к активному сопротивлению.
На резонансной частоте полное сопротивление контура равно активному, а реактивное – нулю. Это объясняется тем, что на резонансной частоте напряжения на L и C равны по значению и противоположны по фазе, поэтому взаимно компенсируются. Наибольший ток в контуре наблюдается на резонансной частоте.
Комплексная передаточная функция напряжения
| Кu (jω) = ŮC / Ů1 = [1/(jωC)]/Zвх = –j Q ωо /[ω(1 + jξ)]. | (19) |
Соответственно, амплитудно-частотная и фазо-частотная характеристики запишутся следующим образом:
| Кu (ω) = Q ωо /ω √(1 + ξ2), φ(ω) = - π/2 – arctg ξ. | (20) |
В радиотехнических устройствах обычно используют контуры с большой добротностью Q >> 1. В таких контурах частотная характеристика представляет интерес только при небольших расстройках ∆ω = ω – ωо, т.е. когда ∆ω / ω << 1, а ωо≈ ω. При этихпредположениях обобщенную расстройку и амплитудно-частотную характеристику можно представить как
| ξ ≈ Q (2 ∆ω / ωо), Кu (ω) = Q / √(1 + (Q 2 ∆ω / ωо)2. | (21) |
На резонансной частоте ω = ωо максимум амплитудно-частотной характеристики равен добротности контура (амплитуда напряжения на конденсаторе в Q раз больше амплитуды входного напряжения). Поэтому резонанс в последовательном контуре называют также резонансом напряжений. Полоса пропускания контура определяется частотами ω1 и ω2 между которыми
| Кu (ω) = Q / √ 2. |
Из (21) можно определить полосу пропускания, которая равна
| П = ωо / Q. | (22) |
Полоса пропускания контура прямо пропорциональна резонансной частоте и обратно пропорциональна добротности.
Годограф комплексной передаточной функции контура представлен на рис. 21. Так как выходной ток совпадает со входным, передаточная функция тока последовательного резонансного контура Ki = 1.
|
Рис. 21 – Годограф комплексной передаточной функции контура
Задание. Собрать схему, представленную на рис. 20. Изменяя значения R, С и L, снять амплитудно-частотные и фазо-частотные характеристики последовательного контура. Изучить влияние параметров контура на его характеристики – резонансную частоту, добротность, полосу частот.





