2.1. Показати, що при великих об’ємах перше рівняння Дітерічі (0.18) переходить у рівняння Ван-дер-Ваальса.
2.2. Знайти рівняння лінії, на якій лежать точки екстремумів кривих Ван-дер-Ваальса при зміні температури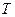 
як параметра.
2.3. Показати, що максимум знайденої в попередній задачі лінії відповідає таким значенням (критичним) змінних:
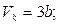
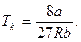
2.4. Яку долю кількості теплоти, що надається ідеальному газу, становить здійснювана ним робота в процесі ізобарного розширення.
2.5. Визначити рівняння політропи ідеального газу в змінних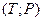 
, вважаючи 
.
2.6. Визначити теплоємність ідеального газу в процесі 
.
2.7. Знайти різницю теплоємностей 
для ідеального парамагнетика, розглянутого в задачі 8 цього розділу.
2.8. Вирахувати різницю 
для одного моля газу Ван-дер-Ваальса, якщо відомо, що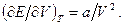 
2.9. Знайти термічне рівняння стану системи, у якої термодинамічні коефіцієнти стиснення 
і розширення 
дорівнюють:
а постійні коефіцієнти 
задовольняють співвідношенню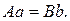 
Розділ 3
ДРУГЕ НАЧАЛО ТЕРМОДИНАМІКИ
Теоретичні відомості
Формулювання другого начала для рівноважних процесів. Друге начало термодинаміки встановлює існування у кожної рівноважної системи нової однозначної функції стану - ентропії, яка зберігає своє значення за будь-яких рівноважних процесів в адіабатично ізольованій системі.
Оскільки друге начало є емпіричним законом, воно допускає різні, але еквівалентні формулювання. Часто його пов’язують з неможливістю існування вічного двигуна другого роду, тобто такого періодично діючого пристрою, який би без компенсації повністю перетворював в роботу теплоту, взяту від якогось тіла. Під компенсацією в термодинаміці розуміють передачу системою частини теплоти іншим тілам у процесі перетворення її в роботу. Роль “інших тіл” у теплових машинах, як правило, відіграє навколишнє середовище.
Фізичною основою другого начала, що призводить до введення ентропії, є принципова нерівноцінність процесів перетворення роботи в теплоту, і теплоти в роботу; процесів, як прийнято їх позначати, 
і 
. Виявляється, що роботу можна завжди прямо і без втрат перетворити в теплоту, тоді як перетворити теплоту в роботу без компенсації (тобто без втрат) неможливо. Це твердження можна формально зобразити так:
, (3.1)
що також еквівалентне другому началу.
Безпосередньо ж існування ентропії, як нової функції стану, випливає з так званого принципу адіабатної недосяжності (ПАН) Каратеодорі, відповідно до якого навколо кожного стану системи існують такі стани, які недосяжні з нього адіабатним рівноважним шляхом. Отже, логіка вимагає введення нової функції для кількісного розрізнення тих станів, про які говориться в ПАН. Якщо позначити таку функцію стану через 
, то еквівалентність тверджень 
і 
для адіабатних процесів призводить до пропорційності цих величин:
(3.2)
Оскільки 
повний диференціал, коефіцієнт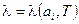 
можна інтерпретувати як інтегруючий множник для елементарної кількості теплоти 
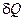. Якщо розглядати температуру за абсолютною шкалою, найбільш проста реалізація для 
є
. (3.3)
У цьому випадку функцію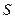 
і називають ентропією. Отже, аналітично ентропія 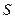визначається диференціальним співвідношенням
(3.4)
Оскільки за другим началом 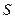є однозначною функцією стану системи, для будь-якого рівноважного циклу повинна виконуватись так звана рівність Клаузіуса:
. (3.5)
Часто (3.5) називають інтегральним формулюванням другого начала, тоді як (3.4) – диференціальним. Якщо система, що здійснює круговий процес, весь час знаходиться при постійній температурі (тобто в контакті з термостатом), з (3.5) і (2.3) знаходимо
, (3.6)
тобто робота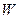 
системи при ізотермічному рівноважному круговому процесі дорівнює нулю. Цей результат вказує на принципову необхідність існування різниці температур для перетворення теплоти в роботу.
Оборотні і необоротні процеси. За другим началом допускаються процеси, в яких перетворення типу 
супроводжується компенсацією, і неможливі такі процеси, в яких таке перетворення не пов’язане з компенсацією. Звідси виникає розділення всіх процесів у замкненій системі на оборотні та необоротні. За визначенням процес переходу системи з одного стану в інший називається оборотним, якщо повернення цієї системи до вихідного стану можна здійснити без зміни термодинамічного стану оточуючих тіл. І навпаки, такий процес називається необоротним, якщо перехід назад неможливо здійснити без названої зміни в оточуючих тілах.
Важливо підкреслити, що будь-який рівноважний процес – оборотний. Це стає зрозумілим, якщо врахувати, що час 
не є значущим параметром при опису рівноважних термодинамічних процесів. Отже, інверсія 
, тобто фізичне обертання процесу в часі, ніяк не впливає на його властивості, зокрема, на властивість залишатися рівноважним. З логічного обернення твердження “рівноважний” Þ “оборотний” випливає, що необоротні процеси є нерівноважними. Це також випливає з однозначності ентропії 
як функції стану. В цьому розумінні зміна ентропії 
є мірою необоротності процесів у замкненій системі.
Наведемо кілька типових необоротних процесів, пропонуючи читачу самостійно довести цю їх властивість:
а) процеси з тертям;
б) процес розширення газу в порожнечу;
в) процес теплопередачі при скінченній різниці температур;
г) процес дифузії.
Формулювання другого начала для нерівноважних процесів. Логічний аналіз двох елементарних процесів переходу системи з одного стану в інший – спочатку нерівноважним шляхом, а потім рівноважним, призводить до висновку, що відповідні при цьому теплоти 
і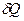 
пов’язані нерівністю 
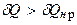, звідки з 
випливає
. (3.7)
Для скінченних процесів переходу із стану 1 в стан 2, інтегруючи (3.7), можна записати
. (3.8)
З (3.7) в свою чергу випливає, що при адіабатних нерівноважних процесах (
) завжди
, 
. (3.9)
Отже, при адіабатних нерівноважних процесах ентропія системи завжди зростає, що і становить друге начало термодинаміки для нерівноважних процесів. Оскільки практично всі природні процеси проходять із скінченною швидкістю, тобто нерівноважні, в адіабатно замкнених системах такі процеси завжди супроводжуються зростанням ентропії.
Для адіабатно неізольованих систем (
) можна розглянути замкнений нерівноважний процес. У цьому випадку, спрямувавши 2®1, з (3.8) отримаємо
. (3.10)
Цей результат називають нерівністю Клаузіуса. Вона виражає друге начало термодинаміки для нерівноважних процесів в адіабатно неізольованих системах.
Основне рівняння термодинаміки для рівноважних процесів. Об’єднуючи диференціальне формулювання другого начала для рівноважних процесів з першим началом, отримуємо основне рівняння термодинаміки для рівноважних процесів:
. (3.11)
На підставі (3.7) для нерівноважних процесів рівняння (3.11) трансформується в нерівність
. (3.12)
У випадку простої системи з зовнішнім параметром 
з (3.11) маємо
(3.13)
Рівняння (3.11) дозволяє встановити диференціальні співвідношення між калоричним і термічними рівняннями стану. При цьому кількість таких співвідношень дорівнює кількості зовнішніх параметрів системи. Отже, з (3.11) з урахуванням (2.4) можна записати
(3.14)
Через те, що ентропія , як функція стану, є функція змінних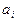 
і 
, тобто 
, маємо
(3.15)
Прирівнюючи коефіцієнти при одноіменних диференціалах в (3.14) і (3.15), знаходимо
(3.16)
і
(3.17)
Диференціюючи (3.16) за 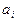, а (3.17) за і прирівнюючи праві частини, після скорочень отримуємо потрібний диференціальний зв’язок між 
та 
:
(3.18)
Для простої системи, коли 
і 
, (3.18) дає
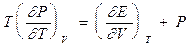. (3.19)
Рівняння (3.18) дозволяє вирахувати різницю теплоємностей 
, а також отримати рівняння адіабатичних процесів різноманітних систем без використання калоричного рівняння стану. Дійсно, формулу (2.10), використовуючи результат (3.18), можна переписати у вигляді:
(3.20)
Зокрема,
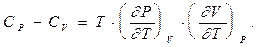(3.21)
Похідні, що входять до (3.21), можна вирахувати, знаючи лише термічне рівняння стану 
, або виміряти, виразивши їх через термічні коефіцієнти 
і 
Вирахування ентропії. Теорема Гіббса. Як видно з розгляду попередніх питань, поняття ентропії з’являється з досить абстрактних міркувань. Крім того, ця величина не є безпосередньо спостережуваною. Ентропіометрів на відміну від термометрів не існує. Однак ентропія є величиною, яку можна вирахувати. Причому інтерес може викликати лише зміна ентропії при переході системи з одного стану в інший. Відповідно до основного рівняння термодинаміки (3.11) при рівноважному переході 
зміна ентропії 
дорівнює
(3.22)
Використовуючи (3.14) і (3.18), докладніше отримаємо
(3.23)
Звідси видно, що для вирахування достатньо знати лише термічні рівняння стану і температурну залежність теплоємності 
. В разі простої системи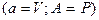 
з (3.23) знаходимо
(3.24)
Так, для одного моля ідеального газу маємо: 
і 
.
З урахуванням наближення для молярної теплоємності 
з (3.24) отримуємо
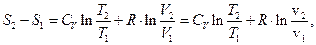(3.25)
де 
об’єм, що припадає на одну частинку газу. Вираз через кращий, оскільки ця величина є більш придатною характеристикою стану, що проявляється в ситуаціях, коли кількість частинок 
перестає бути сталою. Вважаючи початкові параметри 
і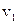 
фіксованими, а кінцеві – змінними: 
, для ентропії одного моля ідеального газу можна записати
або, розширюючи число параметрів,
. (3.26)
Формула (3.26) виражає молярну ентропію. Для 
молів ідеального газу остаточно маємо
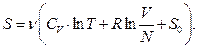(3.27)
Існує твердження, що зветься теоремою Гіббса, згідно з яким ентропія суміші ідеальних газів дорівнює сумі ентропій кожної зі складових цієї суміші при температурі й об’ємі останньої. Через адитивність ентропії ця теорема дійсно справедлива, оскільки можна оборотно (без надання теплоти і затрат на виконання роботи) розділити таку суміш на компоненти, кожний з яких буде займати той самий об’єм, що й до розділення. Ця теорема дозволяє розраховувати зміну ентропії багатокомпонентних ідеальних систем у процесах змішування.
Більш глибокий зміст ентропії розкривається в статистичній фізиці, де, зокрема, показується, що однобічний характер її зміни в замкненій системі визначається переходом системи з менш імовірного стану в більш імовірний.
