Розв’язання. Запишемо рівняння Ван-дер-Ваальса у вигляді

Розкладаючи в ряд за степенями  (з урахуванням:
(з урахуванням:  отримаємо
отримаємо

Порівнюючи з віріальною формою термічного рівняння стану (0.15), знаходимо другий:

і третій:

віріальні коефіцієнти газу Ван-дер-Ваальса.
Задача 5. Визначити рівняння політропи ідеального газу в координатах  вважаючи
вважаючи 
Розв’язання. Скористаємося диференціальним рівнянням політропи (2.11). В нашому випадку  Для ідеального газу з рівняння Менделєєва-Клапейрона знаходимо
Для ідеального газу з рівняння Менделєєва-Клапейрона знаходимо

Підставляючи цей вираз в (2.11) і розділяючи змінні, отримуємо

або
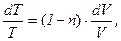
де  - так званий показник політропи.
- так званий показник політропи.
У результаті інтегрування маємо рівняння політропного процесу в координатах (V; T):

або, насамкінець

Для переходу до координат 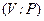 підставимо в попередній результат значення
підставимо в попередній результат значення 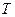 з рівняння Менделєєва-Клапейрона. Отримаємо:
з рівняння Менделєєва-Клапейрона. Отримаємо:

Через те, що  - константи, остаточно знаходимо рівняння політропи в змінних (V; P):
- константи, остаточно знаходимо рівняння політропи в змінних (V; P):

Відзначимо, що, зокрема, для адіабати 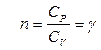 і остання рівність переходить в так зване рівняння Пуассона:
і остання рівність переходить в так зване рівняння Пуассона: 
Задача 6. Яку долю кількості теплоти, що передається ідеальному газу, становить здійснювана ним робота W в процесі політропного розширення.
Розв’язання. Нехай у результаті політропного розширення ідеальний газ змінює свій об’єм від значення  до
до  . При цьому кількість теплоти
. При цьому кількість теплоти 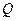 , що була ним отримана, відповідно до першого начала дорівнюватиме
, що була ним отримана, відповідно до першого начала дорівнюватиме

де  – зміна внутрішньої енергії газу,
– зміна внутрішньої енергії газу,  – початкова температура,
– початкова температура,  – кінцева температура. Шуканою величиною в умові є відношення
– кінцева температура. Шуканою величиною в умові є відношення  Для політропного процесу (див. попередню задачу) можна записати
Для політропного процесу (див. попередню задачу) можна записати  де
де  - константа. Отже, роботу
- константа. Отже, роботу 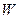 знаходимо у вигляді
знаходимо у вигляді
 .
.
З рівняння Менделєєва-Клапейрона знаходимо початкову і кінцеву температури ідеального газу: 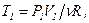
 ; або з урахуванням рівняння політропи:
; або з урахуванням рівняння політропи: 
 Маючи це на увазі, зміну внутрішньої енергії
Маючи це на увазі, зміну внутрішньої енергії  можна записати:
можна записати:

У результаті, підставляючи  і
і  в шукане відношення
в шукане відношення  , отримуємо
, отримуємо

Для  моль (див. задачу 3 розділу 2) маємо
моль (див. задачу 3 розділу 2) маємо  , що остаточно дає
, що остаточно дає

де, нагадуємо,  .
.
Задача 7. Визначити, виразивши через  , теплоємність ідеального газу в процесі
, теплоємність ідеального газу в процесі 
Розв’язання. Звернемо увагу, що цей процес є політропним з показником політропи  Розв’язуючи рівняння
Розв’язуючи рівняння

відносно  , знаходимо:
, знаходимо:

Задача 8. Отримати рівняння адіабати для ідеального парамагнетика, термічне рівняння стану якого виражається законом Кюрі:  а
а 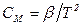 ; тут
; тут  – напруженість магнітного поля,
– напруженість магнітного поля,  - намагніченість,
- намагніченість,  - константи.
- константи.
Розв’язання. Як відомо з електродинаміки, елементарна робота  (віднесена до одиниці об'єму) по збільшенню ізотропною парамагнітною системою своєї намагніченості на величину
(віднесена до одиниці об'єму) по збільшенню ізотропною парамагнітною системою своєї намагніченості на величину  визначається (у гаусовій системі одиниць) формулою
визначається (у гаусовій системі одиниць) формулою

Звідси бачимо, що функцію зовнішнього параметра несе тут величина  , а функцію відповідної узагальненої сили – напруженість
, а функцію відповідної узагальненої сили – напруженість  магнітного поля. Знак “-“ у цій формулі означає, що збільшення намагніченості відбувається за рахунок здійснення роботи над системою.
магнітного поля. Знак “-“ у цій формулі означає, що збільшення намагніченості відбувається за рахунок здійснення роботи над системою.
Скористаємось рівністю (2.7), яка при  перетворюється на диференціальне рівняння адіабати. Отже, в нашому випадку рівняння (2.7) набирає вигляду
перетворюється на диференціальне рівняння адіабати. Отже, в нашому випадку рівняння (2.7) набирає вигляду


Для ідеального парамагнетика  ; крім того на підставі (2.8) і з умови задачі маємо
; крім того на підставі (2.8) і з умови задачі маємо
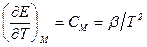 ,
, 
З урахуванням цих рівностей вихідне диференціальне рівняння адіабати отримуємо у вигляді

Розділяючи змінні і інтегруючі, знаходимо шукане рівняння адіабати ідеального парамагнетика в координатах  :
:

Використовуючи термічне рівняння стану 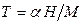 , можна переписати одержане рівняння у координатах
, можна переписати одержане рівняння у координатах  або
або  .
.
Ми розглянули ідеальний парамагнетик. Для нього правомірне дослідження асимптотики  . Як видно з результату, в цьому випадку адіабатному процесу притаманний ефект насичення намагніченості. Елементарний математичний аналіз показує, що при
. Як видно з результату, в цьому випадку адіабатному процесу притаманний ефект насичення намагніченості. Елементарний математичний аналіз показує, що при  , починаючи з деякого значення температури рівняння адіабати не визначає параметрів
, починаючи з деякого значення температури рівняння адіабати не визначає параметрів  і
і  . Це свідчить про те, що вихідні припущення, покладені в умові задачі, справедливі лише для досить високих температур.
. Це свідчить про те, що вихідні припущення, покладені в умові задачі, справедливі лише для досить високих температур.
Задача 9. Знайти рівняння процесу з ідеальним газом, теплоємність якого є лінійною функцією абсолютної температури: 
Розв’язання. З умови маємо
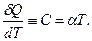
З урахуванням формул (2.7) і (2.8) диференціальне рівняння цього процесу можна записати у вигляді

Оскільки для ідеального газу  це рівняння набирає вигляду
це рівняння набирає вигляду

Розділяючи змінні, отримуємо

звідки після інтегрування остаточно знаходимо рівняння процесу в змінних 

Задача 10. Яку кількість теплоти 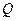 потрібно додати одному молю газу Ван - дер-Ваальса, щоб при розширенні в порожнечу від об’єму
потрібно додати одному молю газу Ван - дер-Ваальса, щоб при розширенні в порожнечу від об’єму  до
до  його температура залишалася незмінною? Вважати
його температура залишалася незмінною? Вважати 
Розв’язання. При розширенні газу в порожнечу робота не здійснюється. Отже, для вказаного процесу з першого начала термодинаміки можна записати 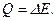
Відповідно до формули (0.30) внутрішня енергія одного моля газу Ван-дер-Ваальса має вираз

Тоді зміну  отримаємо у вигляді (з урахуванням
отримаємо у вигляді (з урахуванням 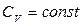 )
)

Оскільки в умові  , остаточно знаходимо шукану кількість теплоти:
, остаточно знаходимо шукану кількість теплоти:







