Якщо навантаження R підключене до активного двополюсника то через нього пройде струм  і буде виділятися потужність:
і буде виділятися потужність:

Вияснимо, яке повинно бути співвідношення між опором навантаження R і вхідним опором двополюсника Rвх, щоб в опорі навантаження виділилася максимальна потужність; чому вона дорівнює і який при цьому к.к.д. передачі. З цією метою визначимо першу похідну Р по R і прирівняємо її нулю:

Звідси
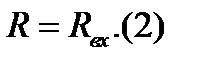
Неважко знайти другу похідну і переконатися в тому, що вона негативна  тому співвідношення 2 відповідає максимум функції P = f (R).
тому співвідношення 2 відповідає максимум функції P = f (R).
Підставивши 2 в 1, отримаємо максимальну потужність, яка може бути виділена в навантаженні R:

Корисна потужність, що виділяється в навантаженні, визначається рівнянням 1. Повна потужність, що виділяється еквівалентним генератором:

Коефіцієнт корисної дії

Якщо  , то
, то 
Якщо потужність Р значна, то працювати з таким низьким к.к.д., як 0,5, абсолютно неприпустимо. Але якщо потужність Р мала і складає всього кілька мілліватт (такою потужністю володіють, наприклад, різні датчики пристроїв автоматики), то з низьким к.к.д. можна не рахуватися, оскільки в цьому режимі датчик віддає навантаженню максимально можливу потужність. Вибір опору навантаження R рівного вхідному опору Rвх активного двополюсника, називають узгодженням навантаження.
19. Синусоїдний струм і основні величини, що його характеризують.(3.1)
Синусоідальний струм представляє собою струм,що змінюється в часі по синусоідальному закону (рис.1):

 рис.1
рис.1
Максимальне значення функції називають амплітудою. Амплітуду струму позначають  ; Період Т- це час,за який виконується одне повне коливання.
; Період Т- це час,за який виконується одне повне коливання.
Частота рівна числу коливань в 1с:

Частоту  вимірюють в герцах (Гц) або
вимірюють в герцах (Гц) або 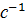 ,кутову частоту в рад/c або
,кутову частоту в рад/c або 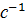 :
:
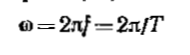
Аргумент синуса, т.е. (  , називають фазою. Фаза характеризує стан коливання(числове значення) в данний момент часу t.
, називають фазою. Фаза характеризує стан коливання(числове значення) в данний момент часу t.
Люба синусоїдально змінна функція оприділяється трьома величинами: амплітудою,кутовою частотою і початковою фазою. У світі найбільше розповсюдження отримали установки синусоідального струму частотою 50 Гц,прийнятою в енергетиці за стандартну.В США стандартною являється частота 60 Гц. Діапазон частот практично застосовуваних синусоїдальних струмів дуже широкий: від долі герца, наприклад в геологорозвідці, до мільярдів герц в електротехніці.
Синусоїдальні струми і е.р.с. порівняно низьких частот(до кількох кільгерц) отримують з допомогою синхронних генераторів(докладніше про них можна дізнатись з курсу електричних машин). Синусоїдальні струми і е.р.с. високих частот отримують з допомогою лампових або напівпровідникових генераторів(більш докладно про них розписано в курсі радіотехніки і менш докладно- в курсі ТОЕ). Принцип отримання синусоідальної е.р.с. шляхом обертання витка з постоянною кутовою швидкістю в рівномірному магнітному полі розглядається на прикладі.(при а=0).Джерело синусоідальної е.р.с. і джерело синусоїдального струму позначають на електричних схемах так же,як і джерела постійної е.р.с. і струму,но над Е і  ставлять крапки.
ставлять крапки.
20. Середнє і діюче значення синусоїдно змінної величини.(3.2)
Під середнім значенням синусоїдно змінної величини розуміють її середнє значення за півперіода. Так, середнє значення струму

Тобто середнє значення синусоідального струму складає 2/π=0,638 від амплітудного. Аналогічно, 
Широко застосовують поняття діючого значення синусоідально змінної величини(його називають також ефективним або середньоквадратичним). Діюче значення струму

Слідуючи з цього,діюче значення синусоідального труму рівно 0,707 від амплітуди. Аналогічно,

Можна співставити теплову дію синусоідального струму струм з тепловою дією постійного струму  , що тече в цей же час по цьому ж опору.
, що тече в цей же час по цьому ж опору.
Кількість тепла,що виділяється за один період синусоїдальним струмом:
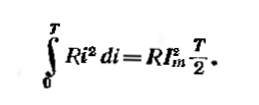
Виділене за той же час постійним струмом тепло рівне  .Прирівняємо їх:
.Прирівняємо їх:

Таким чином, діюче значення синусоїдального струму І чисельно рівне значенню такого постійного струму,який за час,рівний періоду синусоїдального струму,виділяє таку ж кількість тепла,що і синусоїдальний струм.
Більшість вимірювальних приладів показує діюче значення вимірюваної величини)
21. Коефіцієнт амплітуди і коефіцієнт форми.(3.3)
Коефіцієнт амплітуди  - це відношення амплітуди періодично змінної функції до її діючого значення. Таким чином, для синусоїдального струму:
- це відношення амплітуди періодично змінної функції до її діючого значення. Таким чином, для синусоїдального струму:


Під коефіцієнтом форми  розуміють відношення діючого значення періодично змінної функції до її середньому за півперіода значенню. Для синусоїдального струму:
розуміють відношення діючого значення періодично змінної функції до її середньому за півперіода значенню. Для синусоїдального струму:

(для несинусоїдальних періодичних струмів  ,
, 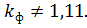 Це відхилення досить точно показує, наскільки несинусоїдальний струм відрізняється від синусоїдального.)
Це відхилення досить точно показує, наскільки несинусоїдальний струм відрізняється від синусоїдального.)
Іноді користуються поняттям коефіцієнта форми несинусоідальної функції,що оприділяється наступним чином:

Де  - середнє по модулю значення струму
- середнє по модулю значення струму
22. Зображення синусоїдно змінних величин векторами на комплексній площині.(3.4)

На рисунку 3.2 дана комплексна площина, на якій можна зобразити комплексні числа. Комплексне число має дійсну(основну) і уявну частини. По осі абсцис комплексної площини відкладають дійсну частину комплексного числа,а по осі ординат – уявну частину. На осі дійсних значень ставимо +1, а на осі уявних значень +j(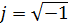 ). З курсу математики відома формула Ейлера
). З курсу математики відома формула Ейлера

Комплексне число  зображають на комплексній площині вектором,чисельно рівним одиниці і зіставними кутом α і віссю дійсних значень (віссю +1). Кут α відраховуєм проти часової стрілки від осі +1. Модуль функції:
зображають на комплексній площині вектором,чисельно рівним одиниці і зіставними кутом α і віссю дійсних значень (віссю +1). Кут α відраховуєм проти часової стрілки від осі +1. Модуль функції:
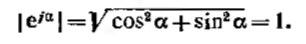
Проекція функції  на вісь +1 рівна cos α, а на вісь +j рівна sin α. Якщо замість функції
на вісь +1 рівна cos α, а на вісь +j рівна sin α. Якщо замість функції  взяти функцію
взяти функцію  , то
, то

На комплексній прощині ця функція, так же ж як і функція  буде зображена під кутом α до осі +1, але величина вектора буде в
буде зображена під кутом α до осі +1, але величина вектора буде в  раз більша.
раз більша.
Кут α в формулі (3.8) може бути любим. Припустимо, що α=  , тобто кут α змінюється прямо пропорційно часу. Тоді
, тобто кут α змінюється прямо пропорційно часу. Тоді

Частина рівняння  представляє собою дійсну частину (Rе) виразу
представляє собою дійсну частину (Rе) виразу  :
:

А функція  є коефіцієнт при уявній частині (Im)
є коефіцієнт при уявній частині (Im)
виразу  :
:

Таким чином, синусоїдально змінний струм і (3.1 і 3.10б) можна представити як Im  ,або що те ж саме, як проекцію обертаючого ся вектора
,або що те ж саме, як проекцію обертаючого ся вектора  на вісь +j(рис. 3.3.):
на вісь +j(рис. 3.3.):
 Історично склалося так, що в радіотехнічній літературі за основу зазвичай застосовують не синусоїду, а косинусоїду,і тому користуються формулою (8.10а)
Історично склалося так, що в радіотехнічній літературі за основу зазвичай застосовують не синусоїду, а косинусоїду,і тому користуються формулою (8.10а)
З ціллю однотипності прийнято на комплексній площині зображати вектори синуідально змінних в часі величин для моменту часу  . При цьому вектор
. При цьому вектор  рівний:
рівний:
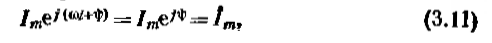
Де  - комплексна величина,модуль якої рівний
- комплексна величина,модуль якої рівний  , а кут, під яким вектор
, а кут, під яким вектор  проведений до осі +1 на комплексній площині, рівний початковій фазі
проведений до осі +1 на комплексній площині, рівний початковій фазі 
Величину  називають комплексною амплітудою струму і. Комплексна амплітуда зображає струм і на комплексній площині для моменту часу
називають комплексною амплітудою струму і. Комплексна амплітуда зображає струм і на комплексній площині для моменту часу  .
.
Комплексна амплітуда
На рис. 23.1. дана комплексна площина, на якій можна зобразити комплексне число. Комплексне число має дійсну і уявну частину. По осі абсцис комплексної площини відкладається дійсну частину Комплексного числа, а по осі ординат – уявну. На осі дійсних значень ставимо +1, а на осі уявних значень 
 .
.

Рис. 23.1
З курсу математики відома формула Ейлера
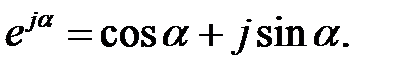
| (23.1) |
Комплексне число  зображають на комплексній площині вектором, чисельно рівним одиниці і який, складає кут
зображають на комплексній площині вектором, чисельно рівним одиниці і який, складає кут  з віссю дійсних значень (віссю +1). Кут
з віссю дійсних значень (віссю +1). Кут  відраховуємо проти годинникової стрілки від осі +1. Модуль функції
відраховуємо проти годинникової стрілки від осі +1. Модуль функції
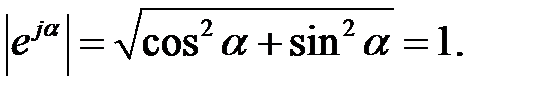
|
Проекція функції  на вісь +1 рівна
на вісь +1 рівна  а на вісь
а на вісь  рівна
рівна  . Якщо замість функції
. Якщо замість функції  взяти функцію
взяти функцію  то
то

|
На комплексній площині ця функція, також як і функція  зображується під кутом
зображується під кутом  до вісі +1, але величина вектора буде в
до вісі +1, але величина вектора буде в  раз більше.
раз більше.
Кут  у формулі (23.1) може бути любим. Допустимо, що
у формулі (23.1) може бути любим. Допустимо, що  тобто кут
тобто кут  змінюється прямо пропорційно часу. Тоді
змінюється прямо пропорційно часу. Тоді

| (23.2) |
Доданок  являє собою дійсну частину (Re) виразу
являє собою дійсну частину (Re) виразу 

| (23.3а) |
а функція  є коефіцієнтом при уявній частині
є коефіцієнтом при уявній частині  виразу
виразу 
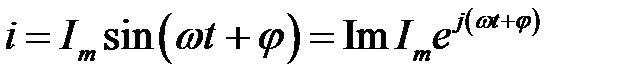
| (23.3б) |
Таким чином, синусоїдально змінний струм  можна представити як
можна представити як  або, що те ж саме, як проекцію вектора, що обертається
або, що те ж саме, як проекцію вектора, що обертається  на вісь
на вісь  (рис 23.2).
(рис 23.2).

Рис. 23.2
З метою уніфікації прийнято на комплексній площині зображати вектори синусоїдальних змінних у часі величин для моменту часу  . При цьому вектор
. При цьому вектор  рівний
рівний

| (23.4) |
де  – комплексна величина, модуль якої рівний
– комплексна величина, модуль якої рівний  а кут, під яким вектор
а кут, під яким вектор  проведений до осі +1 на комплексній площині, рівний початковій фазі
проведений до осі +1 на комплексній площині, рівний початковій фазі 
Величину  називають комплексною амплітудою струму
називають комплексною амплітудою струму  . Комплексна амплітуда зображає струм
. Комплексна амплітуда зображає струм  на комплексній площині для моменту часу
на комплексній площині для моменту часу  .
.
Комплекс діючого значення
На рис. 24.1. дана комплексна площина, на якій можна зобразити комплексне число. Комплексне число має дійсну і уявну частину. По осі абсцис комплексної площини відкладається дійсну частину Комплексного числа, а по осі ординат – уявну. На осі дійсних значень ставимо +1, а на осі уявних значень 
 .
.

Рис. 23.1
З курсу математики відома формула Ейлера
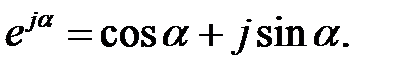
| (24.1) |
Комплексне число  зображають на комплексній площині вектором, чисельно рівним одиниці і який, складає кут
зображають на комплексній площині вектором, чисельно рівним одиниці і який, складає кут  з віссю дійсних значень (віссю +1). Кут
з віссю дійсних значень (віссю +1). Кут  відраховуємо проти годинникової стрілки від осі +1. Модуль функції
відраховуємо проти годинникової стрілки від осі +1. Модуль функції
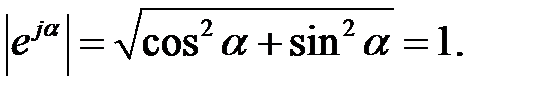
|
Проекція функції  на вісь +1 рівна
на вісь +1 рівна  а на вісь
а на вісь  рівна
рівна  . Якщо замість функції
. Якщо замість функції  взяти функцію
взяти функцію  то
то

|
На комплексній площині ця функція, також як і функція  зображується під кутом
зображується під кутом  до вісі +1, але величина вектора буде в
до вісі +1, але величина вектора буде в  раз більше.
раз більше.
Кут  у формулі (23.1) може бути любим. Допустимо, що
у формулі (23.1) може бути любим. Допустимо, що  тобто кут
тобто кут  змінюється прямо пропорційно часу. Тоді
змінюється прямо пропорційно часу. Тоді

| (24.2) |
Доданок  являє собою дійсну частину (Re) виразу
являє собою дійсну частину (Re) виразу 

| (24.3а) |
а функція  є коефіцієнтом при уявній частині
є коефіцієнтом при уявній частині  виразу
виразу 
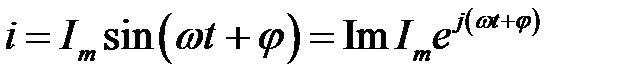
| (24.3б) |
Таким чином, синусоїдально змінний струм  можна представити як
можна представити як  або, що те ж саме, як проекцію вектора, що обертається
або, що те ж саме, як проекцію вектора, що обертається  на вісь
на вісь  (рис 24.2).
(рис 24.2).

Рис. 24.2
З метою уніфікації прийнято на комплексній площині зображати вектори синусоїдальних змінних у часі величин для моменту часу  . При цьому вектор
. При цьому вектор  рівний
рівний

| (24.4) |
де  – комплексна величина, модуль якої рівний
– комплексна величина, модуль якої рівний  а кут, під яким вектор
а кут, під яким вектор  проведений до осі +1 на комплексній площині, рівний початковій фазі
проведений до осі +1 на комплексній площині, рівний початковій фазі 
Величину  називають комплексною амплітудою струму
називають комплексною амплітудою струму  . Комплексна амплітуда зображає струм
. Комплексна амплітуда зображає струм  на комплексній площині для моменту часу
на комплексній площині для моменту часу  .
.
Під комплексом діючого значення струму, чи під комплексом струму (комплексним струмом),  розуміють частку від ділення комплексної амплітуди на
розуміють частку від ділення комплексної амплітуди на 

| (24.5) |






