Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

Для определения значений φ(x) можно воспользоваться специальной таблицей.
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна
P(k1;k2)=Φ(x'') - Φ(x')
Здесь

- функция Лапласа

Значения функции Лапласа находят по специальной таблице.
Пример. Найти вероятность того, что событие А насту пит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение. По условию, n=243; k = 70; р =0,25; q= 0,75. Так как n=243 - достаточно большое число, воспользуемся локальной теоремой Лапласа:

где х = (k—np)/ √npq.
Найдем значение х
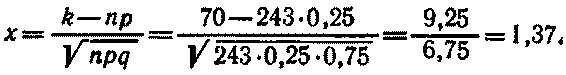
По таблице п найдем ф(1,37) =0,1561. Искомая вероятность
P(243)(70) = 1/6,75*0,1561 =0,0231.
№11 Дискретные и непрерывные случайные величины. Законы распределения
Глава 5. Случайные величины
5.1. Понятие случайной величины
В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом (x>X). Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:
| F (х) = Р(Х < х). | (5.1) |
где х – произвольное действительное число.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
 . .
|
Далее рассматриваются отличия между дискретной и непрерывной случайными величинами.






