Мета роботи: визначити експериментальне відношення теплоємностей повітря.
Прилади та матеріали: прилад Клемана-Дезорма, манометр, насос.
Теоретичні відомості
Стан газу може бути охарактеризований трьома величинами — параметрами стану, тиском р, об'ємом V, температурою Т. Рівняння, що пов'язує ці величини, називається рівнянням стану газу.
Рівнянням стану ідеального газу є рівняння Менделеєва-Клапейрона, яке для одного моля газу має вигляд:
pV=RT, (1)
де R — молярна газова стала.
Теплоємність газів залежить від умов нагрівання. З'ясуємо цю залежність, використовуючи рівняння стану (1) і перший закон термодинаміки, який формулюється так: кількість теплоти dQ, що передається системі, витрачається на збільшення її внутрішньої енергії dU і на роботу dA, що виконує система проти зовнішніх сил:
dQ=dU+Da. (2)
За означенням теплоємність дорівнює:
. (3)
З рівняння (3) видно, що теплоємність може мати різні значення в залежності від способів нагрівання газу, тому що одному і тому ж значенню dT можуть відповідати різні значення dU і dA Елементарна робота дорівнює:
dA=pdV. (4)
Розглянемо процеси, що протікають в ідеальному газі при зміні температури, коли маса газу залишається незмінною і дорівнює одному молю. Кількість теплоти, що необхідна для нагрівання одного моля газу на 1°С, називається молярною теплоємністю.
Процес, що протікає при постійному тискові p=const, називається ізобаричним. Для цього випадку формула (3) буде мати вигляд:
. (5)
З рівняння (1) одержимо
pdV+Vdp=RdT. (6)
Але p=const і dp=0, тому pdV=RdT. Підставляючи це значення в рівняння (5) і замінивши dU на CvdT, одержимо
Cp=Cv+R. (7)
Процес називається ізохоричним, якщо об'єм газу при зміні температури залишається незмінним, тобто V=const. У даному випадку dv=0. Отже, dA=0, тобто при цьому вся теплота, що підводиться до газу, іде на збільшення його внутрішньої енергії. Тоді з рівняння (3) випливає, що молярна теплоємність газу при постійному об'ємові:
.
Ізотермічним називається процес, що протікає при постійній температурі T=const. У цьому випадку dT=0 і dQ = dA, тобто внутрішня енергія газу залишається постійною, і вся теплота, що підводиться, витрачається на роботу.
Процес, що протікає без теплообміну з зовнішнім середовищем, називається адіабатичним. Оскільки dQ=0, перший закон термодинаміки буде мати вигляд:
dU+dA=0.
або
dA=-dU=-CvdT,
тобто при адіабатичному процесі розширення або стискання робота виконується газом тільки за рахунок зміни запасу внутрішньої енергії.
Виведемо рівняння адіабатичного процесу (рівняння Пуассона). Виходячи з того, що dA=-dU, dA=pdV і dU=CvdT, маємо:
рdV=-CvdT. (8)
Поділивши рівняння (6) на (8) і враховуючи (7), одержимо:
або
,
де 
.
Інтегруючи останній вираз, після потенціювання одержимо рівняння Пуассона:
pVg = const.
Величину 
можна визначити за допомогою приладу Клемана-Дезорма (рис. 7.1.1), що складається з теплоізольованого балону А з повітрям при атмосферному тискові ра, насоса та рідинного манометра М. У балон при закритому крані К накачують повітря. Тиск повітря в балоні підвищиться і стане рівним:
Р1=Ра+h1,
де h1 — надлишок тиску повітря в балоні.
Нехай маса повітря після закачування насосом в посудину об'ємом V дорівнює m. Коли кран відкривають, то частина повітря виходить. Позначимо масу повітря, що виходить через Dm, тоді маса повітря, що залишилась, m1=m-Dm.
Маса повітря m, що знаходиться в балоні, займала перед відкриттям крану об'єм V1 менший, ніж V. Оскільки процес короткочасний і значного теплообміну між газом і стінками балона немає, його можна вважати адіабатичним. Згідно з рівнянням Пуассона для маси газу m1 одержимо:
. (9)
Внаслідок адіабатичного розширення газу температура його знизиться, а потім в результаті теплообміну температура газу через невеликий проміжок часу стане рівною кімнатній. При цьому тиск газу підвищиться до величини р3=ра+p2. Початковий і кінцевий стан газу розглядається при однаковій температурі. Тому на основі закону Бойля-Марютта
P1V1=p3V. (10)
Розв'язуючи рівняння (9) і (10) відносно у, знаходимо:
. (11)
Розкладемо lg p1 і lg р3 в ряд Тейлора і підставимо ці значення в формулу (11). Остаточно одержимо:
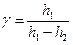. (12)
Рис. 7.1. 1
Хід роботи
1. В балон накачати насосом невелику кількість повітря. При закачуванні повітря, що стискується під поршнем насоса, нагрівається, тому перед початком вимірювання необхідно почекати 2...3 хвилини, поки, завдяки теплообміну, температура в балоні стане рівною кімнатній. Після цього виміряти манометром надлишковий тиск повітря h1 в міліметрах рідинного стовпа.
2. Відкрити кран К і в момент, коли рівні рідини в обох колінах манометра зрівняються, швидко закрити кран. Почекавши 2...3 хвилини, поки газ, охолоджений при адіабатичному розширенні, нагріється до кімнатної температури, виміряти надлишковий тиск h2. Слід пам'ятати, що h1 і h2 розраховуються як різниця висот рідин в обох колінах U – подібного манометра.
3. Величини h1 і h2 відповідно п. п. 1 і 2 виміряти декілька разів і дані записати в таблицю.
| Номер п/п | |||||||
| h1 | |||||||
| h2 |
