МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
УЖГОРОДСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
МАРИНЕЦЬ В.В., РЕГО В.Л.
РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ
(МЕТОДИЧНА РОЗРОБКА З ПРАКТИЧНИХ ЗАНЯТЬ)
ЧАСТИНА ІІ
Рівняння параболічного типу.
Рівняння еліптичного типу.
Теорія потенціалу.
УЖГОРОД 2009
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
УЖГОРОДСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
МАРИНЕЦЬ В.В., РЕГО В.Л.
РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ
(МЕТОДИЧНА РОЗРОБКА З ПРАКТИЧНИХ ЗАНЯТЬ)
ЧАСТИНА ІІ
Рівняння параболічного типу.
Рівняння еліптичного типу.
Теорія потенціалу.
УЖГОРОД 2009
- 3 -
Дана методична розробка складена у відповідності до затвердженої Навчально-методичним управлінням по вищій освіті 23 січня 1985 року проґрами (індекс УМУ-20/190) дисципліни “Рівняння математичної фізики” для студентів державних університетів зі спеціальності 0101 – математика та 0102 – прикладна математика.
Основна мета посібника – допомогти студенту навчитися розв’язувати задачі по двох розділах вказаної дисципліни:
а) рівняння параболічного типу;
б) рівняння еліптичного типу та теорія потенціалу.
В посібнику викладені необхідні короткі теоретичні відомості з даних розділів, розв’язані типові задачі, складені завдання для аудиторної та самостійної роботи. На початку кожної теми наводиться перелік питань, які студент повинен вивчити, і дається посилання на літературу зі вказівкою параґрафів та сторінок.
- 4 -
ТЕМА ІV
РІВНЯННЯ ПАРАБОЛІЧНОГО ТИПУ
Вивчити*:
1. Фізичні процеси, які приводять до рівнянь параболічного типу.
2. Постановка змішаних задач для рівняння теплопровідності.
3. Поширення тепла в однорідному ізотропному скінченому стержні. Метод відокремлення змінних (метод Фур’є).
4. Змішані задачі зі стаціонарними неоднорідностями для рівняння теплопровідності.
5. Загальна схема методу відокремлення змінних для рівняння теплопровідності.
6. Єдиність розв’язку змішаної задачі для рівняння теплопровідності та його неперервна залежність від початкової та крайових умов.
7. Постановка задач Коші для рівняння теплопровідності.
8. Фундаментальний розв’язок однорідного рівняння теплопровідності. Формула Пуассона та її фізична інтерпретація.
9. Єдиність розв’язку задачі Коші для рівняння теплопровідності.
10. Змішані задачі для напівнескінченого стержня з теплоізольованою бічною поверхнею та методи їх інтеґрування.
Розв’язати задачі: №№ 24-26, 34-36, 72-74, 85, 86 (стор. 51-62 згідно [6]), або №№ 7-11, 15б, 15в, 19, 26-29 (розділ ІІІ, тема 3 згідно [4]).
* [3], розділ ІІІ, §§1-3, стор. 184-238, або [4], розділ ІІІ, стор. 165-199.
- 5 -
ТЕОРЕТИЧНІ ВІДОМОСТІ
Постановка змішаних задач для рівнянь параболічного типу
При дослідженні фізичних процесів різної природи часто зустрічаються ДРЧП параболічного типу. Так, наприклад, рівнянням
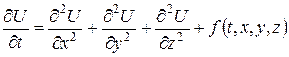
описуються такі процеси:
а) поширення тепла в однорідному ізотропному тілі. Тоді U(t,x,y,z) є температура точок тіла в різні моменти часу, 
(k> 0 – коефіцієнт внутрішньої теплопровідності тіла, c - його питома теплоємність, ρ – густина), 
, де F(t,x,y,z) – інтенсивність внутрішніх джерел тепла;
б) дифузія рідини або газу в однорідному середовищі. Тоді U(t,x,y,z) є концентрація речовини в точках середовища в різні моменти часу, 
(d – коефіцієнт дифузії, c – коефіцієнт пористості середовища), 
, де F(t,x,y,z) – інтенсивність внутрішніх джерел речовини.
При складанні математичних моделей фізичних процесів, які відбуваються в об’єктах скінчених або напівнескінчених розмірів, окрім рівняння та початкової умови необхідно задавати режими на краї об’єкта (крайові умови), що приводить до змішаних задач для ДРЧП.
Для прикладу розглянемо наступну задачу: дослідити процес поширення тепла в однорідному ізотропному стержні довжини 
з теплоізольованою бічною поверхнею, початкова температура якого рівна 
, а на кінцях
1) задані закони зміни температури 
і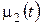 
;
2) задані теплові потоки 
і 
;
3) відбувається теплообмін із навколишнім середовищем, температура якого рівна 
, з коефіцієнтами теплопровідності 
і 
(додатні сталі).
Відповідна математична модель: в області 
знайти розв’язок рівняння теплопровідності
(1)
який справджує початкову умову
та відповідні крайові умови:
1) 
(перша змішана задача);
2) 
(друга змішана задача);
3) 
(третя змішана задача).
- 6 -
Якщо 
то кажуть, що на кінцях стержня підтримується нульова температура. Якщо ж 
то кінці стержня є теплоізольованими.
Аналоґічно ставляться змішані задачі для рівнянь параболічного типу і у випадку довільної вимірності простору.
Нехай, наприклад, потрібно визначити температуру однорідного ізотропного тіла V в довільний момент часу t> 0, якщо початкова температура точок тіла задана функцією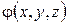 
, усередині тіла є джерела тепла інтенсивності 
, а на його досить гладкій поверхні S заданий один iз наступних теплових режимів:
1) задана температура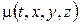 
;
2) заданий тепловий потік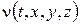 
;
3) проходить теплообмін із навколишнім середовищем, температура якого рівна 
.
Математична модель поставленої задачі буде мати наступний вигляд: в області 
знайти розв’язок ДРЧП
який справджує початкову умову
та одну з крайових умов:
1) 
2) 
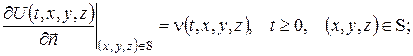
3) 
де h=const> 0 – коефіцієнт теплообміну.
Примітка. Рівняння (1) описує процес поширення температури у стержні з теплоізольованою бічною поверхнею. Якщо ж через бічну поверхню стержня проходить теплообмін із навколишнім середовищем, температура якого рівна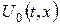 
, то згідно закону Ньютона кількість тепла, яка пройде через бічну поверхню стержня, пропорційна різниці температур стержня і навколишнього середовища, тому рівняння теплопровідності матиме вигляд
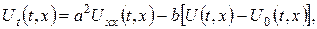(2)
де 
(
– коефіцієнт зовнішньої теплопровідності,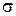 
– периметр поперечного перерізу, 
– площа поперечного перерізу стержня).
Рівняння (2) можна спростити, ввівши підстановку
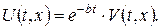
- 7 -
Тоді для нової невідомої функції 
одержимо рівняння
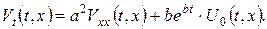
Проте при розв’язуванні конкретних задач дана підстановка не завжди доцільна. Зокрема, у випадку задач зі стаціонарними неоднорідностями після такої підстановки одержуємо складнішу нестаціонарну задачу.
