Способы решения НТС. Расчет ветра в полете. Способы определения угла сноса и путевой скорости

Существуют следующие способы решения навигационного треугольни­ка скоростей:

· графический;

· аналитический;

· с помощью НЛ-10М, расчетчика или наколенного планшета летчика НПЛ-М;

· с помощью вычислительных устройств комплексных навигационных систем;

· приближенно расчетом в уме.

Исходными данными для расчета являются заданный путевой угол (ЗПУ), истинная воздушная скорость полета V, высота полета Н, направление δ и скорость ветра U на высоте полета. На основании этих данных для каждого этапа маршрута рассчитываются угол сноса, путевая скорость и курс полета.

Рассмотрим порядок расчета элементов НТС различными методами.

Пример. Определить угол сноса (УС), путевую скорость (W) и курс полета (К), если заданный путевой угол ЗПУ=100º, истинная воздушная скорость V=800 км/ч, направление ветра δ=60º, скорость ветра U=100 км/ч.

а) Графический способ расчета.

Этот метод заключается в графическом пост­роении НТС по известным его элементам с последующим измерением (с учетом масштаба построения) искомых элементов.

Для графического определения необходимо:

1. Выбрать масштаб чертежа с учетом величин скоростей V и U.

2. Провести линию меридиана, на которой отметить произвольную точку О начала линии заданного пути. С помощью транспортира отложить величину ЗПУ=100º и в этом направлении провести линию заданного пути ОВ. Следует помнить, что по линии заданного пути в полете должен быть направлен вектор путевой скорости (самолет находится на ЛЗП). Таким образом, направление путевой скорости задано, но неизвестна его величина.

С

Д

А

О

К

ЗПУ

δ

B

УС

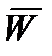
3. Из точки О под углом δ провести линию и в выбранном масштабе отложить на ней величину вектора скорости ветра ОА. Так как является геометрической суммой и 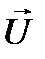, из конца вектора вектором 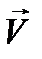как радиусом сделать засечку на линии заданного пути. Полученная точка В укажет конец вектора 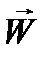. Затем измерить расстояние ОВ и с учетом масштаба определить величину путевой скорости (в примере W=875км/ч).

4. Из точки О провести линию ОД // АБ. Линия ОД определяет требуемое направление вектора , т. е. курс самолета. Измерив транспортиром угол СОД, получим курс (в примере К = 105º).

5. Для определения величины угла сноса УС измерить транспортиром угол ВОД между векторами и 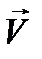( 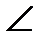ВОД=5º). Знак угла сноса определить по расположению векторов 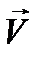и . В примере он отрицателен (УС= -5º, снос влево).

Решение НТС графически может производиться с помощью ветрочета и расчетчика НПЛ-М, которые позволяют изобразить и решить любой навигационный треугольник.

б) Аналитический способ расчета.

Этот метод расчета может применяться при отсутствии расчетных устройств. Для расчета необходимо:

1.Определить угол ветра: УВ = δ − ЗПУ.

Нужно иметь в виду, что угол ветра изменяется от 0º до 360º. Поэтому, если δ меньше ЗПУ, то к УВ следует прибавить 360º. В приведенном примере

УВ = 60º − 100º + 360º = 320º.

Необходимо обратить внимание на правильность определения УВ, так как ошибки в его вычислении приводят к неверным результатам. Кроме того, по величине УВ нужно сделать предварительный вывод о знаке угла сноса и возможной величине путевой скорости (больше или меньше воздушной).

2.Определить угол сноса:

для нашего примера

3. Вычислить курс полета: К = ЗПУ − (± УС) = 100º − (−5º) = 105º.

4. Определить путевую скорость: W = V + UcosУВ = 800 + 100 · cos 320º = 876 км/час.

Аналитический способ расчета элементов НТС используется не только для непосредственных расчетов, но и для контроля расчетов другими методами.

 

в) Расчет элементов НТС в уме.

Расчет элементов НТС в уме выполняется в следующем порядке:

1. Определить угол ветра: УВ = δ − ЗПУ.

2. Вычислить в уме максимальный угол сноса:

3. Определить фактический угол сноса: УСфакт = УСмакс · sin УВ.

Знаки углов сноса и слагаемых путевой скорости определяются по величине угла ветра. При УВ менее 180º, УС будет положительным, более – отрицательным. Слагаемые W будут иметь знак положительный. При углах ветра равным 90º, 270º ─ W ≈ V.

При расчете УС и W в уме значения синусов и косинусов углов в виде коэффициентов берутся из таблицы:

УВº (Ветер попутный)	УСº фактический	W км/час	УВº (ветер встречный)
		V ± U
30 (330)	± 0,5 УС макс	V ± 0,9 U	150 (210)
45 (315)	± 0,7 УС макс	V ± 0,7 U	135 (225)
60 (300)	± 0,9 УС макс	V ± 0,5 U	120 (240)
	± УС макс	V

 

4. Определить, пользуясь таблицей, W по приближенной формуле:

W ≈ V + U · cos УВ.

5. Определить курс следования: Ксл = ЗПУ − (± УС).

Пример. Определить УС,W и Ксл, если ЗПУ = 280º, Vист = 400км/час, δ = 340º, U = 60км/час.

1. Определить угол ветра: УВ = δ − ЗПУ = 340º − 280º = 60º.

2. Определить максимальный угол сноса:

3. Из таблицы найти: УСфакт = 0,9 УСмакс = 0,9 · 9º = 8,1º;

W = V + 0,5 U = 400 + 0,5 · 60 = 430км/час.

4. Определить курс следования:

Ксл = ЗПУ − (± УС) = 280º − (+ 8º) = 272º