Предпринимались и предпринимаются многочисленные попытки вывода количественных соотношений для термодинамических свойств растворов. В основном они ориентированы на согласование с экспериментом в более широком диапазоне концентраций, чем классическая теория Дебая —Хюккеля. Эти попытки можно разделить на два больших направления: эмпирическое или полуэмпирическое и теоретическое, базирующееся на методах статистической и квантовой физики.
Первое направление исходит из анализа некоторых установленных опытным путем закономерностей и возможности их обобщения. Так, например, по Г. Харнеду и Б. Оуэну, экспериментальные данные по коэффициентам активности в интервале концентраций до 4 М хорошо описываются уравнением
. (3.5.1)
Полуэмпирический подход, предложенный Г. И. Микулиным, основан на следующем уравнении для свободной энергии раствора электролита:
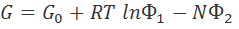, (3.5.2)
где G0 отражает свойства воды и электролита в бесконечно разбавленном растворе; функция Φ1 зависит только от концентрации образующих раствор частиц; N - число молей электролита; функция Φ2 находится в сложной зависимости от концентрации раствора, температуры и давления и отражает отклонение реального раствора от идеального.
Для концентрированных растворов функция Φ2 может быть выражена как
, (3.5.3)
где а и b— коэффициенты, зависящие от давления, температуры и природы электролита.
Используя уравнение (3.5.3), можно рассчитать коэффициенты активности электролита и другие его термодинамические характеристики в концентрированных растворах, а также решить задачу о том, каким должно быть распределение плотности зарядов вокруг иона.
Подход А. Питцера представляет собой модификацию теории Дебая-Хюккеля путем учета короткодействующих сил серией вириальных коэффициентов (они являются подгоночными параметрами) по концентрации. Коэффициенты были табулированы А. Питцером для большого числа различных электролитов. Для 1,1-электролитов они обеспечивают согласие с экспериментом при концентрациях до 3–6 М, для несимметричных электролитов — как правило, до 1–2 М.
Большое число теоретических работ посвящено уточнению классической модели теории Дебая-Хюккеля за счет учета следующих эффектов: собственного объема ионов; изменения диэлектрической проницаемости вблизи ионов вследствие диэлектрического насыщения растворителя и (или) макроскопической диэлектрической проницаемости в объеме раствора в зависимости от концентрации; изменения количества «свободного» растворителя; изменения энергии сольватации ионов и структуры раствора с концентрацией. К этому же направлению следует отнести и рассмотренные в разделе 3.4 теоретические подходы к описанию ассоциации ионов (неполной диссоциации), а также родственные подходы к учету специфического взаимодействия ионов. Однако в каждой из такого рода работ учитывают, как
правило, только один или два из перечисленных эффектов, что не позволяет описать всю совокупность свойств растворов без привлечения дополнительных соображений, не учтенных в исходных посылках теории.
Эффективный учет на полуэмпирическом уровне большой группы обсуждаемых эффектов может быть проведен в рамках модели квазикристаллической решетки. Нижняя граница концентраций, при которой имеет смысл эта модель, определяется путем расчета среднего расстояния между ионами в растворе d. Поскольку величина 1/x обратно пропорциональна c, а величина d обратно пропорциональна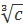 
, соотношение между 1/х и d изменяется при изменении концентрации. В водном растворе 1,1-валентного электролита при температуре 25°C, когда ε = 78,3, 1/х = 0,304с–1/2 ,а d = 0,94 с–1/3(1/х и d в нм при [c] = моль/л), а потому равенство 1/х = d выполняется при концентрации c*= 1,14•10–3М. Если c > c*, то 1/х < d, и наоборот: если c < c*, то 1/х > d.
При концентрациях, превышающих c*, в рамках модели размытой квазикристаллической решетки энергию взаимодействия между ионами с точностью до постоянного множителя можно рассчитать по формуле, аналогичной формуле (3.2.6), но с заменой 1/х на d. Если, как и в теории Дебая-Хюккеля, отклонение от идеальности в растворе электролита связывать только с электростатическими взаимодействиями ионов, то для логарифма коэффициента активности нетрудно получить уравнение вида
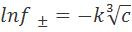, (3.5.4)
которое впервые еще в 1918 г. (т.е. до создания теории Дебая-Хюккеля) было предложено в работе Дж. Гхоша. Опытные данные для водных растворов электролитов в интервале концентраций от 0,01 до 0,1М хорошо согласуются с формулой (3.5.4).
Наибольший интерес на современном этапе представляют работы другого теоретического направления, в которых пытаются рассчитать термодинамические и динамические свойства растворов исходя из концепции их ионно-молекулярной структуры, с использованием общего статистического аппарата Гиббса. Большинство таких работ базируется на методе коррелятивных функций Боголюбова (см. раздел 3.6). Необходимым условием проведения реалистичных расчетов такого рода является знание
микроскопического строения растворов и взаимосвязи его с наблюдаемыми на опыте термодинамическими величинами. В завершение этого раздела необходимо упомянуть не получившие широкого распространения подходы, основанные на небольцмановских законах распределения. В них при вычислении плотности заряда, подставляемой в уравнение Пуассона, используются распределения Ферми-Дирака или Бозе-Эйнштейна.
Итоговое выражение для коэффициента активности аналогично формулам Икеды и Робинсона-Стокса
,
где ns - число гидратации соли, т.е. 
а0—активность воды;
s =1000/(M0m) - число молей воды, приходящихся на один моль безводного растворяемого вещества.
