Описание и изучение современных теорий без знания предыдущих классических считаю бесполезным, поэтому начну с того, что было раньше и почему это не устраивает современную науку.
Развитие теоретических представлений о строении растворов началось с теории электролитической диссоциации Аррениуса. Эта теория, сформулированная в 1887 г., включает следующие основные положения.
1. При растворении молекулы неорганических и органических кислот, оснований и солей спонтанно диссоциируют на ионы, например:
НCl ↔ Н+ + Cl–;
NaOH ↔ Na+ + ОН–;
NaCl ↔ Na+ + Cl–;
СF3СООН ↔ CF3COO– + Н+;
K2SО4 ↔ 2K+ + SO42−.
Ионы представляют собой заряженные частицы, которые состоят или из отдельных атомов, или из группы атомов. Предполагалось, что ионы в растворе ведут себя подобно молекулам идеального газа, т. е. не взаимодействуют друг с другом. Физические причины, которые приводят к диссоциации электролитов, в теории Аррениуса не рассматривались. Не обсуждался также и вопрос о том, почему заряженные частицы, на которые должны были бы распространяться законы электростатики, не взаимодействуют друг с другом в растворах.
2. Диссоциация молекул на ионы является неполной, т. е. не все молекулы электролита, а лишь некоторая их доля α, названная степенью диссоциации, распадается на ионы; доля молекул, равная (1–α), остается недиссоциированной. Таким образом, если при диссоциации одной молекулы электролита образуется ν ионов, то концентрация ионов в растворе оказывается равной ναс, а концентрация недиссоциированных молекул — (1 – α)с. Следовательно, общая молярная концентрация частиц в растворе
составит (1 – α)c + ναc = c[l +α(ν – 1)]. Выражение [1 + α(ν – 1)] показывает, во сколько раз увеличивается общая молярная концентрация частиц в растворе за счет диссоциации электролита, т. е. эквивалентно по своему физическому смыслу изотоническому коэффициенту Вант-Гоффа i. Поэтому по теории Аррениуса i = l + α(ν – 1). (1.1.1)
Поскольку ν>1, а α>0, то i> 1, и уравнение (1.1.1) позволяет дать разумное объяснение экспериментальным данным по осмотическому давлению, по изменению давления пара над растворами, а также по снижению температуры замерзания и по повышению температуры кипения растворов электролитов по сравнению с чистыми растворителями.
3. К процессу электролитической диссоциации применим закон действующих масс. Так, если в результате диссоциации молекулы электролита МА получается один катион М+ и один анион A– (МА↔M+ + А–), то концентрации молекул и ионов равны соответственно:
[МА] = с(1 – α); [M+] = [A–] = αc,
и для константы электролитической диссоциации K по теории Аррениуса получаем следующее выражение:
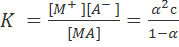. (1.1.2)
Поскольку обратная величина молярной концентрации V = 1/c называется разведением, то уравнение (1.1.2) или аналогичное уравнение с заменой c=1/V называется законом разведения Оствальда.
По теории Аррениуса константа K является постоянной для данного электролита. Поэтому по уравнению (1.1.2) можно рассчитать степень диссоциации в зависимости от концентрации электролита. Решая квадратное уравнение и учитывая, что α > 0, получаем:
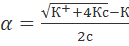(1.1.3)
Как следует из уравнения (1.1.3), при условии K >> 4с α→1, т.е. электролит становится полностью диссоциированным. С другой стороны, при малых константах диссоциации и при не очень низких концентрациях, когда K << 4с,
. (1.2.4)
Соотношения (1.1.2) – (1.1.4) применимы только для растворов симметричных бинарных электролитов (т. е. если одна молекула электролита дает один катион и один анион). Если же электролит имеет несимметричный валентный тип или имеется смесь электролитов, то математические соотношения, описывающие закон действующих масс согласно теории Аррениуса, и вытекающие из них следствия усложняются.
Теория Аррениуса позволила трактовать любые явления, связанные с ионными равновесиями, и легла, таким образом, в основу качественного и количественного анализа
