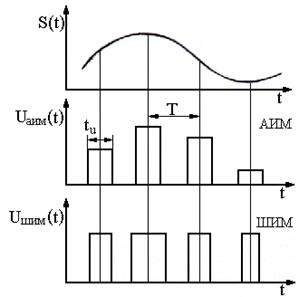
В рассмотренных выше видах модуляции в качестве переносчика информации использовалось гармоническое колебание. Однако в этом качестве можно использовать периодическую последовательность коротких прямоугольных импульсов. При этом возможны такие виды импульсной модуляции: по амплитуде (АИМ) (рис. 1. 22 б.); по ширине или длительности (ШИМ) (рис. 1.22 в.); по частоте (ЧИМ) (рис. 1.22 г.); по фазе (ФИМ); кодо-импульсная (КИМ).(рис.1.22,д).
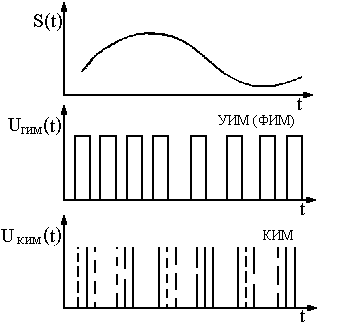
Рис.1.22
Если по закону передаваемого сообщения изменяется амплитуда импульсов, то имеет место амплитудно-импульсная модуляция. При этом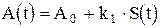 
, где 
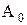—амплитуда немодулированных импульсов, 
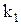—коэффициент пропорциональности между модулирующим напряжением и изменением амплитуды импульсов. При ШИМ по закону передаваемого сообщения применяется длительность импульсов: 
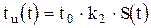, где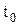 
— длительность немодулированных импульсов, 
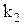— коэффициент пропорциональности между S(t) и изменением длительности импульсов. При изменении частоты следования импульсов будет иметь либо ЧИМ, либо ФИМ: 
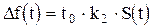, где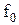 
—частота следования немодулированной импульсной последовательности. Различие между ФИМ и ЧИМ аналогично различию между ФМ и ЧМ гармонических колебаний. При кодо-импульсной модуляции передача сигнала заменяется передачей последовательности чисел. Через интервал времени передаются не отдельные импульсы, а кодовые комбинации импульсов (рис. 1.22 д.).
Немодулированная последовательность импульсов представляется рядом Фурье. Для получения спектра сигнала при импульсной модуляции в этом случае надо представить соответствующее выражение модулируемого параметра.
Рассмотрим АИМ гармоническим управляющим сигналом. В этом случае по закону управляющего сигнала изменяется амплитуда импульсов.
Определим спектр полученного сигнала.
Известно, что последовательность прямоугольных импульсов одинаковой амплитуды и длительности, которая в данном случае выступает в роли несущего колебания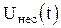 
, можно разложить в ряд Фурье 
,
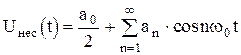где
|
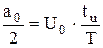—постоянная составляющая, 
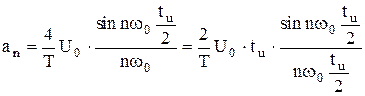— амплитуда n-ой гармоники,
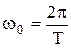—частота следования импульсов в последовательности,
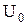—амплитуда импульса.
Рис.1.22
Тогда
.
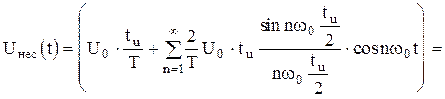
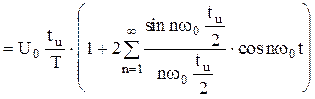При амплитудной модуляции последовательности прямоугольных импульсов получим:
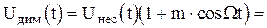
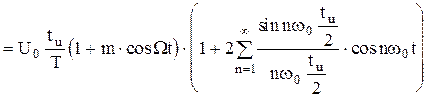. (1.36)
При АИМ каждая частотная составляющая немодулированной последовательности импульсов модулируется как “изолированная” несущая (рис.1.23).
Рис.1.23
Ширина спектра получается безграничной, но на практике достаточно передавать лишь первый “лепесток” т.е. иметь полосу пропускания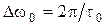 
. Ширина полосы частот при импульсной модуляции практически не зависит от вида модуляции и определяется минимальной длительностью импульса.
