Импульсов
Вычислить комплексные амплитуды гармонических составляющих для колебаний вида:
|
Рисунок 1.7
Определим комплексную амплитуду n-ой гармоники:
(1.7)
Так как при n=0,2,4,..., А =0, то постоянной составляющей и четных гармоник данное колебание не содержит.
При n=1; n=3; n=5:
Перейдем от комплексных амплитуд к мгновенным значениям гармоник и представим заданный сигнал в виде суммы гармонических составляющих:
Представление периодического сигнала в виде совокупности гармоник называется отысканием спектра.
Зависимость спектра от изменения параметров последовательности импульсов
Рассмотрим характер изменения спектра от изменения периода и длительности импульсов.
1. Сравним спектры двух последовательностей с одинаковыми
|
длительностями и амплитудами импульсов, но разными периодами: 
(рисунок 1.8).
|
Рисунок 1.8
а) ширина участка спектра не изменяется, так как она зависит от длительности импульса 
.
б) расстояние между гармониками увеличивается, так как 
.
в) число гармоник на одном участке спектра уменьшается: 
.
г) величина постоянной составляющей и амплитуды гармоник увеличиваются (в определенных рамках).
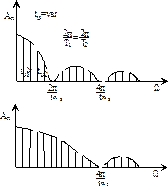
2. Сравним спектры при 
; 
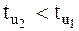(рисунок 1.9).
|
|
Рисунок 1.9
а) ширина одного участка спектра от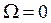 
до 
изменяется; при уменьшении 
ширина возрастает.
б) расстояние между гармониками не изменяется 
в) число гармоник на одном участке спектра увеличивается 
.
ВЫВОД. Ширина участка спектра тем больше, чем меньше длительность импульса; гармоники тем ближе друг к другу, чем больше период. Амплитуда гармоник уменьшается при увеличении периода.
Распределение мощности в спектре периодического сигнала
Пусть несинусоидальный периодический ток i (t) протекает по активному сопротивлению R (рисунок 1.10). Определить среднюю за период мощность, которая расходуется на этом сопротивлении.
I(t)
Средняя за период мощность определяется соотношением:
U(t) R 
. (1.8)
Рисунок.1.10. Разложим функцию тока i(t) в ряд Фурье:
,
Подставим это разложение в выражение (1.8):
,
Учитывая, что 
, а интегрирование за период исходной функции гармонических колебаний с удвоенной частотой и произведений косинусов и синусов дают нуль, получим:
.
Так как 
— постоянная составляющая тока, а 
— амплитуда n-ной гармоники, то
Средняя мощность периодического колебания выражается бесконечной суммой мощностей спектральных составляющих.
Спектры непериодических сигналов
Спектральная плотность
Пусть задан сигнал S(t), который действует в конечном интервале времени 
. Для проведения гармонического анализа поступим следующим образом:
1) Превратим наш непериодический сигнал в периодический путем повторения его с произвольным периодом Т. Для полученной таким образом функции применимо разложение в ряд Фурье:
где 
–– комплексная амплитуда n-ой гармоники.
Известно, что комплексную амплитуду можно получить из функции S(t) в соответствии с выражением (1.5):
.
2) Предположим, что Т стремится к бесконечности. В пределе получим бесконечно малые амплитуды гармонических составляющих, сумма которых изображает исходную функцию S(t). Количество этих гармоник будет бесконечно большим, а расстояние между гармониками –– бесконечно малым.
Спектр из линейчатого становится сплошным. Выразим это аналитически.
Подставим 
в S(t):
.
так как 
, то
.
При 
величина 
превращается в бесконечно малую dω; 
–– в текущую частоту 
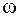, а операция суммирования- в операцию интегрирования, то есть 
.
Таким образом, получим:
.
В этом выражении обозначим второй интеграл через 
. (1.10)
Функция частоты 
называется спектральной плотностью или спектральной характеристикой функции времени S(t).
Подставив в исходное выражение S(t), получим:
. (1.11)
Выражения (1.10) и (1.11) носят названия пары преобразований Фурье, которые связывают между собой функцию времени S(t) и комплексную функцию частоты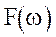 
.
Поясним смысл спектральной плотности 
.
Если сигнал периодический, то n -ая гармоника с частотой 
будет иметь амплитуду 
Если же сигнал непериодический, но в некотором ограниченном интервале совпадает с периодическим S(t),то на частоте 
спектральная плотность равна
.
Отсюда видно, что 
.
Так как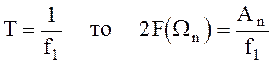 
.
Видно, что значение спектральной плотности на определенной частоте получается путем деления амплитуды n-ой гармоники на полосу частот 
, отделяющую соседние линии дискретного спектра. Таким образом, 
имеет смысл плотности амплитуд (амплитуда: Герц) и определяет величину сигнала, которая приходится на единицу полосы частот шириной в один Герц.
Поэтому эта непрерывная функция частоты и называется спектральной плотностью амплитуд или просто спектральной плотностью.
Огибающая сплошного спектра непериодического сигнала и огибающая линейчатого спектра периодического сигнала совпадают по форме и отличаются масштабом.
Спектральную плотность можно представить в комплексной форме:
, (1.12)
где 
.
Модуль спектральной плотности равен 
; аргумент 
.
Спектр непериодического сигнала характеризуется зависимостью модуля и аргумента спектральной плотности от частоты. В отличии от рассмотренных ранее дискретных спектров периодических колебаний, этот спектр является сплошным, так как описывается непрерывными функциями частоты 
и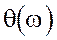 
: (рисунок 1.11).
Рисунок 1.11- Зависимости модуля и аргумента спектральной плотности от частоты
