При угловой модуляции по модуляции по закону управляющего сигнала изменяется текущая фаза 
.В зависимости от того, какой из параметров изменяется (частота 
или 
фаза) различают две разновидности угловой модуляции: частотную или фазовую. Эти виды модуляции имеют много общего. Рассмотрим каждый из них.
Фазовая модуляция. Управляющее напряжение изменяет фазу ВЧ-колебания, а амплитуда остается постоянной.
; 
(1.24)
где 
— начальная фаза; 
—коэффициент пропорциональности, связывающий изменение фазы с управляющим сигналом.
Следовательно
(1.30)
Примем 
.
Модуляция по фазе всегда сопровождается изменением частоты колебаний. Для выяснения этого обстоятельства запишем 
в ви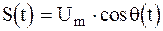де 
, где 
— текущая фаза.
Мгновенная угловая частота колебаний 
определяется как скорость изменения угла 
во времени, то есть 
. В свою очередь 
. Подставляя значение в выражение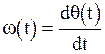 
получим: 
.
Таким образом изменение фазы 
при фазовой модуляции в соответствии с выражением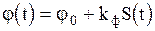 
приводит к изменению частоты на величину 
.
Если управляющий сигнал изменяется по гармоническому закону 
,то мгновенное значение изменения формы на величину 
приводит к изменению частоты на величину 
. Фазомодулированное колебание можно представить в следующем виде:
(1.31)
где 
— индекс фазовой модуляции; величина его определяет максимальное отклонение фазы ВЧ-колебании при модуляции от первоначального значения (при отсутствии модуляции).
Частотная модуляция. При ЧМ переменным параметром, изменяющимся по закону управляющего сигнала, является частота то есть
(1.32)
где 
; 
-коэффициент пропорциональности, связывающий изменение частоты с управляющим сигналом.
Получим аналитическое выражение для ЧМ сигнала. Для этого воспользуемся соотношением 
.
Нам задана частота , нужно найти аргумент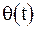 
. Известно, что 
или 
.
Следовательно 
.
Из этого выражения следует, что при ЧМ фаза колебаний также является величиной переменной: 
Если управляющий сигнал изменяется по гармоническому закону 
,то аналитическое выражение для ЧМ сигнала примет вид: 
; 
, (1.34)
где 
— изменение или девиация частоты при модуляции.
Видно, что изменение частоты по закону 
приводит к изменению фазы по закону 
.
Величина 
называется индексом частотной модуляции. Проведенный анализ показывает, что фазовая и частотная модуляции имеют много общего: в обоих случаях происходит взаимосвязанное изменение фазы и частоты колебаний. ЧМ и ФМ можно рассматривать как две разновидности так называемой угловой модуляции, при которой по закону управляющего сигнала изменяется угол 
. Тональной модуляции разницы между ЧМ и ФМ нет. Различия проявляются сложных управляющих сигналах. Это различие определяется тем фактом, что фазовый сдвиг между ФМ-сигналом и немодулированным колебанием пропорционален (ф.1.30), в то время как для ЧМ-сигнала этот сдвиг пропорционален интегралу от управляющего сигнала (ф.1.33).
Спектр ЧМ-колебания. ЧМ-колебание изменяется по закону 
.
Для определения спектра заменим косинус суммы двух углов: 
.
1.Определим спектр ЧМ-колебания при малом индексе модуляции 
.
В этом случае
, 
.
Поэтому
.
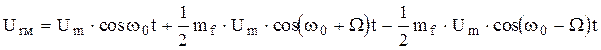Замечаем что при малом индексе модуляции спектр ЧМ-колебания отличается от спектра АМ-колебания только сдвигом фазы нижней боковой частоты на 180 градусов (рис.1.21 а).
2.Определим спектр ЧМ-колебания при произвольных индексах модуляции. Для этого периодические функции 
и 
нужно разложить в ряд Фурье, коэффициенты которых являются функциями Бесселя первого рода:
.
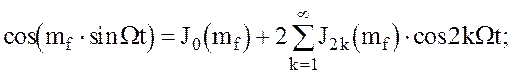
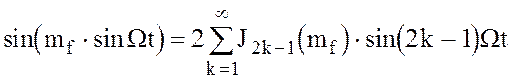Подставляя эти выражения в общее выражение S(t) для ЧМ сигнала (1.34) и выполнив тригонометрические преобразования, окончательно получим
. (1.35)
Таким образом, ЧМ-колебание имеет дискретный спектр и состоит из несущей и бесконечного цикла боковых частот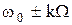 
c амплитудами 
.Однако практически ширина спектра при ЧМ ограничена. Это можно заметить из рисунка 1.20, на котором приведены графики функций 
Рис.1.20
При 
и 
функции 
убывают столь быстро, что ими можно пренебречь, то есть считать, что 
при .
Поэтому ширина спектра при ЧМ будет равна
, 
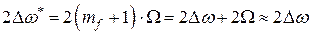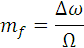
то есть приближенно равна удвоенной девиации частоты. На рисунке 1.21 б в качестве примера показан график спектра ЧМ-колебаний при 
. Таким образом, ширина спектра при ЧМ-колебании в 
раз шире, чем при АМ.
Рис.1.22
