При АМ – модуляции по закону управляющего сигнала S(t) изменяется амплитуда высокочастотных колебаний (рис.1.17);
(1.18)
где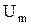 
— амплитуда ВЧ-колебания при отсутствии модуляции; 
— максимальное абсолютное изменение амплитуды ВЧ-колебания;
|
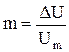— коэффициент амплитудной модуляции, характеризует глубину модуляции.
Рис.1.17 Рис.1.18
При модуляции управляющий сигнал называется также модулирующим.
Аналитически АМ-колебание можно представить в виде произведения изменяющейся по закону огибающей S(t) амплитуды U(t) и гармонического заполнения 
:
Представляя в этом выражение значение U (t) из (1.18), получим аналитическое описание АМ-сигнала:
(1.19)
Если модулирующем является низкочастотное гармоническое колебания,то АМ-сигнал можно представить в виде:
. (1.20)
Такой сигнал называется однотональным АМ-сигналом.
Из рисунка 1.17 видно, что
откуда имеем:
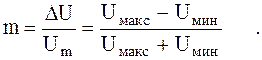
Определим спектр АМ-колебания при однотональной модуляции. Это можно сделать с помощью преобразования Фурье, но проще с помощью простых тригонометрических преобразований. Действительно, пусть 
,тогда 
(1.21)
Замечаем, что АМ-колебание имеет дискретный спектр и состоит из трех некратных гармонических составляющих: колебания несущей частоты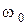 
с амплитудой 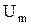и двух колебаний с амплитудами 
и частотами 
.При этом 
называется верхней боковой частотой, а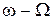 
—нижней боковой частотой. Ширина спектра АМ-колебаний равна 
. Амплитудно-спектральная диаграмма АМ-колебания при однотональной модуляции имеет вид, представленный на рисунке 1.18.
В более общем случае модуляция осуществляется сложным многотональным периодическим сигналом, который можно разложить в ряд Фурье по гармоническим составляющим 
. Спектральная диаграмма модулирующего сигнала изображена на рис. 1.19а.
Выражение для АМ-колебания можно представить в виде:
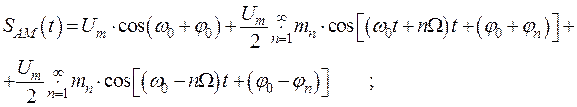(1.22)
где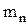 
— парциальные или частные коэффициенты модуляции по каждой гармонике.
Видно, что АМ-колебания состоит из колебания несущей частоты 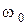и двух боковых полос с суммарными 
и разносторонними 
частотами. Спектральная диаграмма, такого колебания представлена на рисунке 1.19 б.
а) б)
Рис.1.19
Спектр верхних боковых колебаний является масштабной копией спектра модулирующего сигнала, сдвинутой в область высоких частот на величину 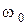. Спектр нижних боковых колебаний также повторяет спектральную диаграмму сигнала S(t), но располагается спектрально несущей .
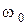Если спектр модулирующего сигнала ограничен сверху частотой FМАКС , то ширина спектра модулированного колебания равна 2 FМАКС .
