Методические указания
Виды связей между признаками
Существующие между признаками связи принято классифицировать на функциональные (жёстко детерминированные) и статистические (стохастически детерминированные).
Связь признака у с признаком х называется функциональной, если каждому возможному значению независимого признака х соответствует одно или несколько строго определённых значений зависимого признака у.
Функциональную связь можно представить уравнением:
,
где yi – результативный признак;
– известная функция связи результативного и факторного признаков;
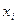– факторный признак.
Стохастическая связь — это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины x или других величин x1, x2, …, xn (случайных или неслучайных).
В случае корреляционной связи среднее значение (математическое ожидание) случайной величины результативного признака у закономерно изменяется в зависимости от изменения другой величины х или других случайных величин x1, x2, …, xn. Такая связь проявляется не в каждом отдельном случае, а во всей совокупности в целом, и только при достаточно большом количестве наблюю-дений становится очевидным, вызывает ли изменение значений случайного признака х изменение распределения средних величин случайного признака у. Корреляционная связь является частным случаем стохастической связи.
На первом этапе корреляционно-регрессионного анализа устанавливается факт наличия связи и её форма. На втором этапе измеряется теснота связи и проводится оценка её существенности. На заключительном этапе – построение модели связи (уравнения регрессии).
Измерение тесноты связи
Для установления факта наличия связи и её формы используют различные методы.
Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции (r). При любой форме зависимости (линейной или криволинейной) рассчитывается эмпирическое корреляционное отношение (
).
Линейный коэффициент корреляции рассчитывается следующим образом:
или 
где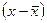 
– отклонения вариантов признака-фактора от их средней величины;
– отклонения вариантов значений результативного признака от их средней величины;
– число единиц в совокупности;
– среднее квадратическое отклонение соответственно признака-фактора и результативного признака.
Эмпирическое корреляционное отношение определяется по формуле
где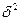 
– межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора.
– общая дисперсия результативного признака.
Линейный коэффициент корреляции может принимать значения в пределах от –1 до +1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак при этом указывает на направление связи: «+» говорит о прямой связи, «–» – об обратной. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1; чем ближе значение к 1, тем теснее связь, направление связи оно не показывает.
Оценка существенности линейного коэффициента корреляции при большом объёме выборки свыше 500 проводится с использованием t -критерия Стьюдента, который представляет собой отношение отношения коэффициента корреляции (r) к его средней квадратической ошибке (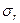
):
,
где 
.
При недостаточно большом объёме выборки величина средней квадратической ошибки коэффициента корреляции определяется по формуле
.
Уравнение регрессии
Если это отношение окажется больше значения t -критерия Стьюдента, определяемого по Приложению 5 при числе степеней свободы k = n – 2 и с вероятностью (1 – a), то следует говорить о существенности коэффициента корреляции при уровне значимости а = 0,01 или 0,05.
Квадрат коэффициента корреляции r2 называется коэффициентом детерминации и показывает, на сколько процентов вариация результативного признака обусловлена вариацией признака-фактора.
После установления достаточной степени тесноты связи выполняется построение модели связи (уравнения регрессии). Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии. Чаще всего используются следующие типы функций:
1) линейная 
;
2) гиперболическая 
;
3) параболическая 
;
4) показательная 
.
Для определения численных значений параметров уравнения связи (линии регрессии) используется метод наименьших квадратов и решается система нормальных уравнений.
Для определения параметров уравнения прямолинейной корреляционной связи система нормальных уравнений (для несгруппированных данных) имеет вид:
Параметры а и b можно определить и по следующим формулам
; 
.
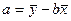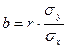Для проверки возможности использования линейной функции в качестве модели связи определяется разность (ŋ2−r2). Если она менее 0,1, то считается возможным применение линейной функции. Для решения этой же задачи можно использовать величину ω2, определяемую по формуле
,
где m − число групп, на которое разделён диапазон значений факторного признака.
Если ω2 окажется меньше табличного значения F- критерия, то нулевая гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается. Значение F – критерия определяется по таблице в зависимости от уровня значимости а = 0,05 (вероятность Р = 0,95) и числа степеней свободы числителя (k1 = m−2) и знаменателя (k2 = n–m) (приложение В).
В качестве меры достоверности уравнения корреляционной зависимости используется процентное отношение средней квадратической ошибки уравнения Se к среднему уровню результативного признака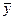 
:
; 
,
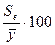где y − фактические значения результативного признака;
− значения результативного признака, рассчитанные по уравнению регрессии;
l − число параметров уравнения регрессии.
Если это соотношение не превышает 10 − 15%, то следует считать, что уравнение регрессии достаточно хорошо отображает изучаемую взаимосвязь.
Решение типовых задач
Пример 7.1
Известны следующие данные о величине оборотного капитала и прибыли по группе предприятий торговли.
| № п/п | Оборотный капитал, тыс. руб. | Прибыль, тыс. руб. | № п/п | Оборотный капитал, тыс. руб. | Прибыль, тыс. руб. |
На основе приведённых данных: 1) определим тесноту связи между оборотным капиталом и прибылью и дадим оценку существенности линейного коэффициента корреляции; 2) построим уравнение регрессии и оценим возможность использования линейной функции.
Решение
1. Факторный признак – величина оборотного капитала (x); результативный признак – прибыль (y).
Предполагая, что зависимость между оборотным капиталом и прибылью имеет линейную форму, определим тесноту связи на основе линейного коэффициента корреляции. Данные для расчёта приведены во вспомогательной таблице 1:
Вспомогательная таблица 1
| № п/п | Оборот-ный капитал, тыс. руб. (х) | При-быль, тыс. руб. (у) | x2 | y2 | xy |
| 
| 
|
| 143,6 | -16,6 | 275,56 | ||||||
| 104,4 | -18,4 | 338,56 | ||||||
| 180,4 | 3,6 | 12,96 | ||||||
| 94,0 | -12 | 144,00 | ||||||
| 152,4 | -15,4 | 237,16 | ||||||
| 108,8 | 1,2 | 1,44 | ||||||
| 213,6 | -20,6 | 424,36 | ||||||
| 182,8 | 7,2 | 51,84 | ||||||
| 212,8 | -28,8 | 829,44 | ||||||
| 196,4 | -7,4 | 54,76 | ||||||
| 155,6 | -20,6 | 424,36 | ||||||
| 190,4 | -15,4 | 237,16 | ||||||
| 112,4 | 2,6 | 6,76 | ||||||
| 224,4 | -14,4 | 207,36 | ||||||
| 185,6 | -16,6 | 275,56 | ||||||
| 228,4 | -13,4 | 179,56 | ||||||
| 263,6 | 0,4 | 0,16 | ||||||
| 260,8 | -19,8 | 392,04 | ||||||
| 230,4 | 4,6 | 21,16 | ||||||
| 161,2 | 5,8 | 33,64 | ||||||
| 222,8 | 52,2 | 2724,84 | ||||||
| 189,2 | -32,2 | 1036,84 | ||||||
| 176,8 | -12,8 | 163,84 | ||||||
| 267,6 | 46,4 | 2152,96 | ||||||
| 273,6 | 12,4 | 153,76 | ||||||
| Итого | 93731,14 | 10380,08 |
Линейный коэффициент корреляции составит:
Значение линейного коэффициента корреляции 0,95 свидетельствует о прямой и тесной связи между величиной оборотного капитала и прибылью предприятий торговли.
Чтобы это утверждать, дадим оценку существенности линейного коэффициента корреляции на основе расчёта t-критерия Стьюдента:
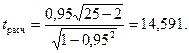
Показатель tтабл находим по таблицам Стьюдента (приложение Б).
Для числа степеней свободы К = n−2=25−2=23 и уровня значимости 1% tтабл = 2,797; 14,591 > 2,797.
Следовательно, с вероятностью 0,99 можно утверждать существенность коэффициента корреляции.
2. В случае линейной связи параметры уравнения регрессии 
определяются следующим образом:
; .
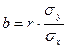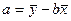Используя данные таблицы 1, рассчитаем среднее значение факторного и результативного признака, дисперсию и среднее квадратическое отклонение.
Среднее значение факторного признака:
тыс. руб.
Дисперсия факторного признака:
.
Среднее квадратическое отклонение факторного признака:
тыс. руб.
Среднее значение результативного признака:
тыс. руб.
Дисперсия результативного признака:
.
Среднее квадратическое отклонение результативного признака:
руб.
Теперь можем определить параметры уравнения регрессии:
;
.
Подставим значения параметров в уравнение регрессии:
.
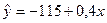Коэффициент регрессии b = 0,4 говорит о том, что при увеличении оборотного капитала на 1 тыс. руб. прибыль в среднем возрастет на 0,4 тыс. руб., или на 400 руб.
Возможность использования линейной функции может быть оценена на основе величины:
,
где m − число групп, на которое разделен диапазон значений факторного признака.
Для расчёта ω2 необходимо исчислить эмпирический коэффициент детерминации:
Для определения межгрупповой дисперсии произведём группировку по факторному признаку и выполним вспомогательные расчёты (таблица 2).
Таблица 2 – Группировка предприятий по величине оборотного капитала
| № п/п | Оборотный капитал, тыс. руб. | Число предприятий | Середина интервала (Xi) | Прибыль в среднем на одно предприятиe 
|
| 510 − 600 | 98,25 | |||
| 600 − 690 | 141,5 | |||
| 690 − 780 | 175,43 | |||
| 780 − 870 | 218,67 | |||
| 870 − 960 | 276,25 |
Межгрупповая дисперсия:
Тогда эмпирический коэффициент детерминации оставит:
.
Значение эмпирического коэффициента детерминации говорит о том, что на 87,6% вариация прибыли в этой совокупности предприятий обусловлена вариацией оборотного капитала и на 12,4% – вариацией прочих неучтенных факторов.
Тогда 
составит:
.
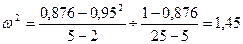При уровне значимости а = 0,05 (вероятность Р =0,95), и числа степеней свободы числителя 3 (k1 = m -2 = 5 - 2 = 3), и знаменателя 20 (k2 = n – m = 25-5 = 20) (приложение В) F табл= 3,10. Так как ω2 меньше табличного значения F- критерия, то нулевая гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается.
В качестве меры достоверности уравнения корреляционной зависимости используется процентное отношение средней квадратической ошибки уравнения Se к среднему уровню результативного признака :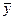
; ,
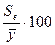где у − фактические значения результативного признака;
− значения результативного признака, рассчитанные по уравнению
регрессии;
l — число параметров уравнения регрессии.
Теоретические значения по уравнению регрессии находим следующим образом: фактическое значение х = 634 тыс. руб. подставляем в уравнение регрессии = −110 + 0,4 x => = −110+0,4 х ∙634 = 143,6; для остальных значений оборотного капитала расчёт теоретических значений величины прибыли производится аналогично. Вспомогательные расчёты для определения средней квадратической ошибки уравнения регрессии приведены в таблице 1.
Полученное соотношение не превышает 15%, а это значит, что уравнение регрессии достаточно хорошо отображает изучаемую взаимосвязь и может быть использовано для прогнозов.
