Исследованию нестационарных процессов предшествует предварительное преобразование системы дифференциальных уравнений к стандартному виду – к форме Коши.
Покажем один из способов такого преобразования. В результате такого преобразования система уравнений приводится к канонической форме, удобной для представления в виде эквивалентной структурной схемы, привычной при исследовании систем автоматического управления.
Пусть дифференциальное уравнение порядка n в операторной форме, описывающее процессы в системе, представлено в виде:

(20)
где p = d/dt – символ дифференцирования;
x(t), y(t) – вход и выход системы;
ai, bj – коэффициенты полиномов, в общем случае функции времени; i = [1 – n]; j = [1 – m]; m £ n.
Правую часть выражения (20) умножим и поделим на pn (pn / pn) и получим:

(21)
где
 (22) или
(22) или 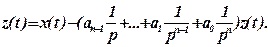 (23)
(23)
Полученные зависимости (21) - (23) являются представлением исходного уравнения (20) в канонической форме.
Используя эти зависимости, а именно - (21) и (23) – легко может быть получена эквивалентная структурная схема, моделирующая данную систему, которая представлена на рисунке 5.
 |
Приведем примеры использования описанного метода представления дифференциальных уравнений.
Пример 1.
Интегро - дифференцирующее динамическое звено описывается следующим операторным уравнением (первого порядка):

(24)
Приведем его к стандартной форме (20)

(25)

где
 |
Соответствующая структурная схема, реализующая данное уравнение и получаемая из схемы для общего случая (см. рисунок 5), имеет вид:
Пример 2.
Дано операторное уравнение второго порядка:
(26)

Этим уравнением моделируются динамические характеристики инерционного и форсирующего звеньев второго порядка.
Преобразуя, приведем его к стандартной форме и получим

(27)

где
 |
Соответствующая структурная схема, получаемая из схемы для общего случая (см. рисунок 5), имеет вид, представленный на рисунке 7.
Пример исследования нестационарных и нелинейных процессов
Постановка задачи
Провести исследование нестационарной системы, замкнутая структурная схема которой представлена на рисунке 8.
При этом:
· оценить переходные процессы при задании на вход контура слежения скачкообразного, а также синусоидального сигналов;
· построить фазовые траектории ошибки Δ.
 |
 ;
;  , T2 = 0.05 c.
, T2 = 0.05 c.
Таблица 1. Исходные данные
| t, c | ||||||
| Ko | ||||||
| T1, c | 1.0 | 0.8 | 0.6 | 0.5 | 0.5 | 0.5 |
| K1,1/c | 0. 9 | 0.7 | 0. 5 | 0.4 | 0.4 |
Как следует из рассмотрения приведенных данных, большинство параметров системы является функцией времени. Кроме того, в системе присутствует нелинейность.
Синусоидальный входной сигнал имеетвид: x=A sin (2p f t + j0), A = 0.3, f=0.5 Гц, аскачкообразный сигнал – единичную ступеньку.






