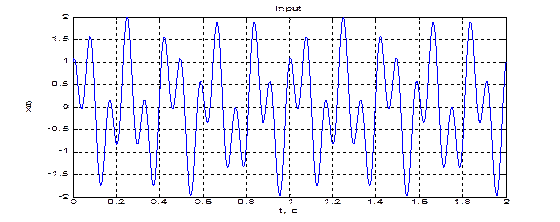
Входной сигнал представим в виде вектора, элементы которого равны значениям функции, являющейся суммой двух синусоид с частотами 5 и 12 Гц. Найти Фурье-изображение этого сигнала и вывести графики входного процесса и модуля его Фурье-изображения:
>> t=0:0.001:2;
>> x=sin(2*pi*5*t)+cos(2*pi*12*t);
>> plot(t,x),grid;
>> title('input');
>> xlabel('t, c');
>> ylabel('X(t)')
>> y=fft(x);
>> a=abs(y);
>> plot(a);grid;
>> title('fourier');
>> xlabel('number');
>> ylabel('absF(X(t))')

Теперь осуществим обратное преобразование с помощью функции ifft:
>> z=ifft(y);
>> plot(t,z), grid;
>> title('inverse');xlabel('number');
>> xlabel('t, c');
>> ylabel('Z(t))')

Как следует из последнего рисунка, воспроизведенный процесс в точности совпадает с исходным.
Из выражений (4) можно заметить:
- номер m соответствует моменту времени tm, в который измерен входной сигнал x(m);
- номер k – это индекс значения частоты fk, которому соответствует найденный элемент y(k) дискретного преобразования Фурье;
- для перехода от индексов к временной и частотной областям, необходимо знать значение шага h дискрета времени, через который измерен входной сигнал x(t), и промежуток T времени, на протяжении которого он измерен; тогда дискрет по частоте в изображении Фурье определяется выражением
Df=1/T,
а диапазон изменения частоты – выражением
F=1/h.
Так в нашем примере Df=0.5, F= 1000.
- Фурье - изображение определяется функцией fft только для положительных частот в диапазоне от 0 до F, что неудобно для построения графиков Фурье – изображения от частоты; более удобным является переход к вектору Фурье – изображения, определенному в диапазоне частот [-F/2 - F/2].
Сформируем для данного примера массив частот и выведем график с аргументом частотой
>> f=0:0.5:1000;
>> plot(f,a)'grid;
>> plot(f,a);grid;
>> title('F(x)');xlabel('friquency, Hz');
>> ylabel('abs(F(X))')

На рисунке трудно различить частоты (5 и 12 Гц), с которыми колеблется входной сигнал.
Для установления истинного спектра входного сигнала необходимо вначале преобразовать полученный вектор y Фурье – изображения с помощью процедуры fftshift. Она предназначена для формирования нового вектора z из заданного у путем перестановки второй половины вектора у в первую половину вектора z
>> f1=-500:0.5:500;
>> v=fftshift(y);
>> a=abs(v);
>> plot(f1(970:1030),a(970:1030));grid;
>> title('F/N');
>> xlabel('friquency, Hz');
>> ylabel('abs(F(X))/N')
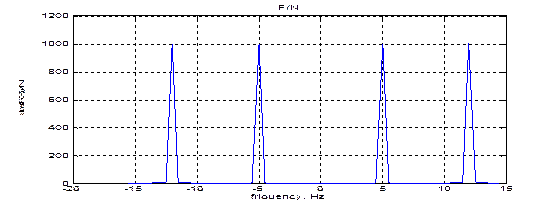
Из графика видно, что в спектре входного сигнала есть две гармоники- 5 и 12 Гц.
Неудобным является то, что по графику невозможно определить амплитуду этих гармоник. Чтобы сделать это, необходимо весь вектор y разделить на число его элементов N:
>> N=length(y);
>> a=abs(v)/N;
>> plot(f1(970:1030),a(970:1030));grid;
>> title('F/N');
>> xlabel('friquency, Hz');
>> ylabel('abs(F(X))/N')

Задание на самостоятельную работу






