В.Г. НОВИКОВ
МОДЕЛИРОВАНИЕ СИСТЕМ
ЛАБАРАТОРНЫЙ ПРАКТИКУМ
Коломна 2007
УДК 519.8 (076)
ББК 22.18
М–74
Рецензенты:
- доктор технических наук, профессор ТРУШКОВ А.С. (Коломенский государственный педагогический институт, Коломна Московской области);
- кандидат технических наук, профессор МЯЛЬДЗИН Н.Х. (Коломенский институт МГОУ, Коломна Московской области);
- кафедра “Автоматики и электроники в машиностроении” Коломенского института МГОУ (Коломна Московской области) (заведующий кафедрой кандидат технических наук, профессор РОДОВ А.М.).
Автором пособия является доктор технических наук, профессор кафедры “Автоматики и электроники в машиностроении” КИ МГОУ Новиков В.Г.
Моделирование систем: Лабораторный практикум/ Новиков В.Г. – Коломна: КИ МГОУ, 2007. – 60 с., ил.
В лабораторном практикуме излагаются методические указания к выполнению лабораторных работ по курсу Моделирование систем, соответствующему Государственным образовательным стандартам высшего профессионального образования по направлению подготовки дипломированного специалиста 220000 – “Автоматика и управление” и бакалавра 220200 – “Автоматизация и управление”.
Для студентов очной и очно-заочной формы обучения по специальности 220201 - Управление и информатика в технических системах, по направлению 220200 - Автоматизация и управление.
Утверждено Учебно-методическим Советом Коломенского института МГОУ, Председатель Совета Липатов А.М.
УДК 519.8 (076)
ББК 22.18
© Новиков В.Г.
© КИ МГОУ, 2007
ВВЕДЕНИЕ.. 5
ТЕМА 1. Исследование линейных стационарных систем с помощью пакета прикладных программ MatLab “ Control Sistem Toolbox” (“Система управления”) 6
1.1. Введение. 6
1.2. Ввод и преобразование моделей. 7
1.2.1. Основные положения. 7
1.2.2. Пример создания модели. 9
1.3. Анализ системы.. 11
1.3.1. Общие положения. 11
1.3.2. Примеры анализа во временной области. 12
1.3.3. Примеры анализа в частотной области. 13
1.3.4. Примеры применения процедур для вычисления полюсов и нулей системы.. 14
1.4. Задание на самостоятельную работу. 15
1.4.1. Структурная схема модели. 15
1.4.2. Требования к исследованию модели. 15
1.4.3. Исходные параметры модели. 16
1.4.4. Отчетность по лабораторной работе. 16
ТЕМА 2. ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ при Исследовании СИСТЕМ с помощью пакета MatLab “ Signal Processing Toolbox ” 17
2.1. Введение. 17
2.2. Общие средства фильтрации. Формирование случайных процессов. 17
2.2.1. Общие основы линейной фильтрации. 17
2.2.2. Формирование случайных процессов. 21
2.3. Спектральный и статистический анализ. 23
2.3.1. Основные понятия. 23
2.3.2. Примеры спектрального анализа. 24
2.4. Задание на самостоятельную работу. 27
2.4.1 Цифровая обработка сигналов. 27
2.4.2. Формирование случайного процесса из белого шума. 27
2.4.3. Формирование процесса как сумма гармоник. 27
2.4.4. Исходные данные. 27
2.4.5. Отчетность по лабораторной работе. 27
ТЕМА 3. МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ с помощью пакета MatLab “ Simulink ”. 29
3.1. Краткие сведения о подсистеме MatLab SIMULINK.. 29
3.1.1. Запуск подсистемы SIMULINK.. 29
3.1.2. Создание модели. 30
3.1.3. Некоторые основные приемы подготовки и редактирования модели. 31
3.1.4. Установка параметров моделирования и его выполнение. 32
3.5.1. Установка параметров моделирования. 32
3.5.2. Выполнение моделирования. 33
3.5.3. Завершение работы.. 33
3.2. Пример создания модели системы и выбор ее характеристик. 33
3.2.1. Постановка задачи. 33
3.2.2. Методика решения. 34
3.2.3. Результаты моделирования. 36
3.3. Задание на самостоятельную работу. 38
3.3.1. Исходная динамическая система. 38
3.3.2. Требования к работе. 38
ТЕМА 4. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ в линейных нестационарных динамических системах с использованием подсистемы MatLab “ Simulink ”. 40
4.1. Краткие сведения из теории линейных нестационарных и нелинейных систем автоматического управления. 40
4.1.1. Особенности процессов в линейных нестационарных системах. 40
4.1.2. Особенности процессов в нелинейных САУ.. 41
4.1.3. Метод фазового пространства. 42
4.2. Моделирования процессов в линейных нестационарных и нелинейных динамических системах с использованием подсистемы MatLab SIMULINK.. 43
4.2.1. Приведение линейного дифференциального уравнения к канонической форме. 43
4.2.2. Пример исследования нестационарных и нелинейных процессов. 45
4.2.3. Методика формирования модели в системе MatLab. 46
4.3. Задание на самостоятельную работу. 50
4.3.1. Исходная система. 50
4.3.2. Требования к работе. 50
4.3.3. Отчетность. 51
ТЕМА 5. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ в динамических системах с использованием подсистемы MatLab “ Simulink ”. 53
5. 1. Введение. 53
5. 2. Пример имитационного моделирования процессов с использованием подсистемы MatLab SIMULINK.. 53
5.2.1. Постановка задачи. 53
5.2.2. Формирование схемы моделирования. 54
5.2.3. Подготовка к имитационному моделированию.. 54
5.3. Задание на самостоятельную работу. 57
5.3.1. Исходная схема. 57
5.3.2. Требования к работе. 57
5.3.3. Отчетность. 58
Использованные источники. 60
ВВЕДЕНИЕ
Данный практикум ориентирован на исследование математических (аналитических и имитационных) моделей, применяемых при проектировании автоматизированных систем управления различных уровней, а также на освоение новой информационной технологии в автоматизации исследования этих сложных систем на базе моделирования на ЭВМ.
Цель практикума – выработать у студентов умение самостоятельно применять для решения конкретных инженерных задач исследования систем знания по моделированию на ЭВМ, полученные из лекционного курса.
Каждая лабораторная работа по дисциплине “Моделирование систем” должна научить студентов:
- самостоятельно решать отдельные прикладные задачи исследования систем на базе метода машинной имитации;
- оформлять результаты машинных экспериментов в соответствии с требованиями ГОСТ;
- защищать результаты, полученные при выполнении лабораторных работ по исследованию характеристик систем на ЭВМ.
Предполагается, что при выполнении лабораторных работ задачи моделирования ограничены рассмотрением вопросов оценки с помощью имитационных экспериментов временных, частотных характеристик для системного исследования функционирования сложных объектов.
В предлагаемом учебном практикуме рассмотрены вопросы организации выполнения лабораторных работ на ПЭВМ, даны конкретные методические указания по выполнению каждой работы. При этом даны:
- краткие теоретические положения по предмету исследования;
- приведены примеры исследования;
- и сформулированы задания на самостоятельную работу.
Методические позиции системного машинного моделирования, рассмотренные для организации лабораторных работ, могут быть полезны студентам в дальнейшем и при выполнении соответствующих курсовых работ, связанных с исследованием сложных систем.
Для практической реализации моделей в практикуме используется система MatLab в среде Windows – 95/98/2000/XP.
Выбор в качестве программной реализации моделей в практикуме этой системы обусловлен тем, что в настоящее время она является одним из наиболее эффективных и распространенных средств моделирования сложных систем на ПЭВМ и успешно используется для моделирования систем
ТЕМА 1. Исследование линейных стационарных систем с помощью пакета прикладных программ MatLab “ Control Sistem Toolbox” (“Система управления”)
Введение
Для решения задач САУ в среде MATLAB используется набор специальных функций, или тулбокс (ToolBox) «Система управления» (Control System Toolbox).
Tулбокс (ToolBox) «Система управления» представляет собой библиотеку алгоритмов, содержащихся в функциональных М-файлах и реализующих наиболее общие методы
- расчета;
- анализа;
- построения (моделирования) систем.
Пакет прикладных программ (ППП) Control System Toolbox сосредоточен в подкаталоге CONTROL каталога TOOLBOX системы MatLab:
MatLab\ TOOLBOX\ CONTROL.
Основными вычислительными объектами этого ППП являются:
· Родительский объект (класс) LTI (Linear Time-Invariant System – линейные, инвариантные во времени системы) или линейные стационарные системы (ЛЛС);
· Дочерние объекты (классы), т.е. подклассы класса LTI, соответствующие трем разным представлениям ЛСС:
- TF – объект (Transfer Function) – передаточная функция);
- ZPK – объект (Zero-Pole-Gain – нули, полюсы, коэффициент передачи);
- SS – объект (State Spaсe пространство состояний).
Объекты различных классов характеризуются:
- класса TF - векторами коэффициентов числителя и знаменателя рациональной передаточной функции;
- класса ZPK – векторами, содержащими значения нулей, полюсов передаточной функции и коэффициента передачи системы;
- класса SS – четверкой матриц, описывающих динамическую систему в пространстве состояния.
Специфические атрибуты передаточных функций ( TF – объектов):
num – Числитель
Для одномерной системы (система с одним входом U и выходом Y) - вектор-строка;
Для многомерной системы (с несколькими входами и выходами) – массив ячеек из векторов-строк размером nY на nU.
den – Знаменатель
Для одномерной системы (система с одним входом U и выходом Y) - вектор-строка;
Для многомерной системы (с несколькими входами и выходами) – массив ячеек из векторов-строк размером nY на nU.
Variable – Имя (тип) переменной.
Специфические атрибуты ZPK – объектов:
z – Нули
Для одномерной системы - вектор-строка;
Для многомерной системы – массив ячеек из векторов-строк размером nY на nU.
p – Полюсы
Для одномерной системы - вектор-строка;
Для многомерной системы – массив ячеек из векторов-строк размером nY на nU.
k – Коэффициент передачи
Для одномерной системы - число;
Для многомерной системы – матрица размером nY на nU.
Специфические атрибуты SS – объектов (моделей пространства состояний):
a, b, c, d – A, B, C, D – матрицы, в соответствии с уравнениями в переменных состояния:
x = Ax + Bu,
y = Cx + Du.
e - E – матрица для систем Descriptor’а (описателя). По умолчанию E= eye (size(A)).
StateName – имя переменной состояния (не обязательное). Массив ячеек nX на 1 из строк.
Атрибуты, общие для всех LTI-моделей:
Ts – Дискрет по времени (в секундах).
Ts = -1 для дискретных систем;
Ts = 0 для непрерывных систем.
Td – Задержка входов (в секундах).
InputName – Имена входов.
Строка - для систем с одним входом.
Массив ячеек nX на 1 из строк – для системы с несколькими входами.
OutpuName – Имена выходов.
Строка - для систем с одним входом.
Массив ячеек nX на 1 из строк – для системы с несколькими входами.
Notes – Заметки.
Userdata – Дополнительная информация или данные.
Ввод и преобразование моделей
Основные положения
Ввод модели линейной стационарной системы (ЛСС) в среду пакета CONTROL возможен в трех формах:
- в форме матриц пространства состояний;
- в виде коэффициентов числителя и знаменателей передаточной функции;
- в форме задания нулей, полюсов и коэффициента передачи системы.
К процедурам создания LTI- моделей относятся:
ss Создает модель пространства состояния по заданным матрицам A, B, C, D уравнений состояния системы.
dss Создает аналогичную модель по описанию пространства состояния более общего вида, когда уравнения переменных состояния не разрешены относительно производных.
tf Создает модель по заданным передаточным функциям системы.
zpk Создает модель по заданным нулям, полюсам и коэффициентам передачи системы.
filt Создает модель по дискретным передаточным функциям системы, записанным в форме полинома от z-1.
set Присваивает значения некоторым другим полям (атрибутам) LTI- объекта (названиям входов и выходов, названиям системы и т.п.).
get Выдает значения атрибутов объекта.
Указанные процедуры позволяют создавать как непрерывные модели, так и дискретные.
В последнем случае к числу входных параметров процедуры следует добавить в конце значения параметра Ts – шага дискретизации, а вводимые значения коэффициентов уже должны задавать параметры дискретных передаточных функций (для tf и zpk), либо матрицы конечно-разностных уравнений пространства состояний (при использовании процедур ss и dss).
При использовании процедуры filt должны задаваться векторы коэффициентов числителя и знаменателя дискретной передаточной функции, представленной в виде отношения полиномов от z-1.
Процедуры ss, dss, tf и zpk применяются также для преобразования моделей из одной из указанных форм в другую.
Модель, заданную как непрерывная, можно преобразовать в дискретную форму, воспользовавшись процедурой c2d в соответствии со схемой:
sysd=c2d(sys, Ts, method).
Здесь sys – исходная непрерывнаязаданная модель;
sysd – получаемый в результате работы процедуры дискретный аналог исходной системы;
Ts – задаваемое значение шага дискретизации;
method – параметр, определяющий метод дискретизации. Например:
‘zoh’ – соответствует применению экстрополятора нулевого порядка: внутри интервала дискретизации сигналы аппроксимируются постоянной величиной, равной значению сигнала в начале интервала дискретизации;
‘foh’ - соответствует применению экстрополятора первого порядка: внутри интервала дискретизации сигналы аппроксимируются отрезками прямых, проходящих через концы кривой сигнала в интервале дискретизации.
Процедура d2c осуществляет обратную операцию – переводит дискретную систему в непрерывную.
Процедура d2d позволяет переопределить дискретную систему, меняя шаг дискретизации:
sys1=d2d(sys, Ts).
Для создания модели нужно предварительно либо перевести уравнения всей системы к форме уравнений пространства состояния, либо найти передаточные функции системы.
В общем случае это довольно сложно.
В то же время реальные САУ состоят из соединенных между собой отдельных блоков (динамических звеньев), уравнения которых достаточно просты.
Поэтому в практике проектирования САУ принято использовать структурные методы, когда САУ задается как определенная схема соединения отдельных элементарных динамических звеньев, и фактически проектируется одно или несколько из этих звеньев таким образом, чтобы обеспечить заданное качество всей системы.
В соответствии с этим в MatLab предусмотрена возможность “набирать” программно схему САУ путем:
- предварительного ввода моделей звеньев, составляющих САУ, и
- последующего “соединения” этих звеньев в единую структуру.
К процедурам, осуществляющим расчет характеристик соединений отдельных звеньев, относятся:
plus (minus) – выполняет параллельное соединении указанных звеньев;
parallel -выполняет ту же процедуру, параллельного соединения звеньев; отличие – может использоваться для многомерных систем и для осуществления параллельного соединения лишь по некоторым входам и выходам
mtimes ( или знак “*” между именами звеньев ) – выполняет последовательное соединении указанных звеньев; применяется для одномерных систем;
series -выполняет последовательное частичное соединении многомерных систем;
feedback -выполняет такое соединении двух звеньев, когда второе указанное звено составляет цепь отрицательной обратной связи для первого звена;
append -выполняет формальное объединение не связанных между собой систем (добавление выходов и входов второй системы к выходам и входам первой);
connect – установление соединений входов и выходов многомерной системы, созданной формальным объединением процедурой append;
inv – рассчитывает САУ, обратную указанной, т.е. такую, у которой выходы и входы поменяли местами.
Пример создания модели
Создать модель движения системы (торпеды) в горизонтальном канале, состоящую из подмодели углового движения вокруг вертикальной оси и из подмодели цепи управления.
При этом подмодель углового движения может быть представлена в виде двух последовательно соединенных звеньев:
- апериодического
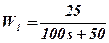 и
и
- интегрирующего
 .
.
В свою очередь подмодель цепи управления может быть представлена в виде двух параллельно соединенных частей:
– части, управляемой гироскопом направления и представляющей собой обычное усилительное звено K;
- части, управляемой гиротахометром, которую можно представить как дифференцирующе-колебательное звено W3.
Соответствующая структурная схема имеет вид, представленный на рисунке,
 |
где M – момент внешних сил относительно вертикали;
ω - угловая скорость торпеды ;
ψ – угол поворота торпеды вокруг вертикали (угол рыскания).
Mу – момент управляющих сил, создаваемый при помощи рулей управления.
Решение.
Подмодель углового движения:
>> W1=tf(25,[100 50])
Transfer function:
---------------
100 s + 50
>> W2=tf(1, [1 0])
Transfer function:
---.
s
Последовательное соединение этих звеньев можно осуществить двумя способами:
– применением процедуры series:
>> W0=series(W1, W2)
Transfer function:
---------------------;
100 s^2 + 50 s
- либо просто операцией “перемножения” моделей:
>> W01=W1*W2
Transfer function:
----------------------.
100 s^2 + 50 s
Теперь сформируем цепь управления, входом которой является угол рыскания торпеды ψ, а выходом – момент Mу, накладываемый на торпеду со стороны ее рулей направления.
Усилительное звено:
>> K=tf(2,1)
Transfer function:
Дифференцирующе-колебательное звено W3:
>> W3=tf([100 0], [1 10 100])
Transfer function:
100 s
-----------------------.
s^2 + 10 s + 100
Параллельное соединение этих двух звеньев управления можно осуществить тоже двумя способами:
- либо используя процедуру parallel
>> U1=parallel(K,W3)
Transfer function:
2 s^2 + 120 s + 200
-------------------
s^2 + 10 s + 100
- либо применяя операцию “сложения” моделей
>> U=K+W3
Transfer function:
2 s^2 + 120 s + 200
------------------------.
s^2 + 10 s + 100
Теперь найдем модель всей САУ угловым движением торпеды, рассматривая цепь управления как цепь отрицательной обратной связи для торпеды, пользуясь для объединения прямой и обратной цепи процедурой feedback:
>> sys=feedback(W01,U)
Transfer function:
25 s^2 + 250 s + 2500
-------------------------------------------------------------------.
100 s^4 + 1050 s^3 + 10550 s^2 + 8000 s + 5000
После того, как система сформирована, можно ввести при помощи процедуры set некоторые ее символьные описания. В частности присвоить названия входам и выходам системы, а также дать краткий комментарий к самой системе.
>> set(sys,'InputName','Момент сил', 'OutputName','Угол рыскания')
>> set(sys,'Notes','Угловое движение торпеды')
>> get(sys)
num: {[0 0 25 250 2.5e+003]}
den: {[100 1.05e+003 1.06e+004 8e+003 5e+003]}
Variable: 's'
Ts: 0
ioDelay: 0
InputDelay: 0
OutputDelay: 0
InputName: {'Момент сил'}
OutputName: {'Угол рыскания'}
InputGroup: [1x1 struct]
OutputGroup: [1x1 struct]
Notes: {'Угловое движение торпеды'}
UserData: []
Анализ системы
Общие положения
Пакет CONTROL предоставляет пакет процедур для осуществления анализа САУ, прежде всего, для определения отклика системы на внешние воздействия как во временной, так и в частотной областях.






