При исследовании гидродинамической структуры потока импульсным методом были получены значения концентрации индикатора на выходе из аппарата представленные в табл. 1.
Таблица 1
Концентрация индикатора на выходе потока из аппарата
| Время ti, мин | ||||||||
| Концентрация Сэ(ti), г/м3 |
Требуется определить среднее время пребывания потока в аппарате и построить кривую отклика в безразмерных координатах.
Решение
Определение значений нормированной кривой отклика 
(табл. 2):
.
Таблица 2
Значения нормированной кривой отклика
| ti, мин | ||||||||
| C(ti), мин–1 | 0,03 | 0,05 | 0,05 | 0,04 | 0,02 | 0,01 |
где n – количество опытов; i – текущий номер опыта;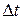 
– интервал времени между двумя ближайшими измерениями.
Определение среднего времени пребывания потока в аппарате:
мин.
Определение безразмерного времени 
и безразмерной кривой отклика 
(табл. 3):
; 
.
Таблица 3
Значения безразмерной кривой отклика
|
| 0,333 | 0,667 | 1,333 | 1,667 | 2,333 | |||
|
| 0,45 | 0,75 | 0,75 | 0,6 | 0,3 | 0,15 |
Построение по данным табл. 3 безразмерной кривой отклика (рисунок).
|
Рис. Безразмерная кривая отклика
Приложение 2
Пример решения дифференциального уравнения методом Эйлера
Как правило, решение модели представляет наиболее сложную задачу, когда ее математическое описание получено в дифференциальной форме. Если аналитического решения нет или оно затруднено, то для получения результата используют численные методы.
Рассмотрим пример решения численным методом уравнения движения частицы в сепарационной зоне кипящего слоя в условиях переменной скорости потока (1).
 , (1)
|
где 
– текущая скорость частицы; 
– текущая скорость потока, как функция высоты подъема частицы, например в диффузоре; 
– коэффициент сопротивления как функция скорости частицы относительно потока;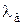 
– коэффициент сопротивления частицы в условиях витания; 
– скорость витания частицы; g – ускорение силы тяжести; Н – текущая высота подъема частицы.
Составим алгоритм решения уравнения (1), предварительно приведя его к следующему виду:
 . (2)
|
Обозначим для удобства правую часть уравнения (2) через f (W, H), тогда в соответствии с методом Эйлера запишем
 . (3)
|
Алгоритм решения уравнения (3) будет следующим:
1. Задание исходных значений и граничных условий:
W по, W 0, W в, W п(H), H 0, dH,lв,l = f (Re);
W п = W по и W = W 0 при H = 0;
W = 0 при H = H max.
2. Определение нового значения скорости частицы W = W + f (W, H) dH.
3. Определение нового значения высоты подъема частицы H = = H + dH.
4. Проверка условия W £ 0, если условие выполняется, то переход к п. 5, в противном случае переход к п. 2.
5. Выход.
Приложение 3
Значения параметра ν для различных уровней значимости
и степеней свободы
| Число степеней свободы, f | Уровни значимости р | Число степеней свободы, f | Уровни значимости р | ||||||
| 0,10 | 0,05 | 0,025 | 0,01 | 0,10 | 0,05 | 0,025 | 0,01 | ||
| 1,406 | 1,412 | 1,414 | 1,414 | 2,326 | 2,493 | 2,638 | 2,800 | ||
| 1,645 | 1,689 | 1,710 | 1,723 | 2,354 | 2,523 | 2,670 | 2,837 | ||
| 1,791 | 1,869 | 1,917 | 1,955 | 2,380 | 2,551 | 2,701 | 2,871 | ||
| 1,894 | 1,996 | 2,067 | 2,130 | 2,404 | 2,577 | 2,728 | 2,903 | ||
| 1,974 | 2,093 | 2,182 | 2,265 | 2,426 | 2,600 | 2,754 | 2,932 | ||
| 2,041 | 2,172 | 2,273 | 2,374 | 2,447 | 2,623 | 2,778 | 2,959 | ||
| 2,097 | 2,237 | 2,349 | 2,464 | 2,467 | 2,644 | 2,801 | 2,984 | ||
| 2,146 | 2,294 | 2,414 | 2,540 | 2,486 | 2,664 | 2,823 | 3,008 | ||
| 2,190 | 2,343 | 2,470 | 2,606 | 2,504 | 2,683 | 2,843 | 3,030 | ||
| 2,229 | 2,378 | 2,519 | 2,663 | 2,520 | 2,701 | 2,862 | 3,051 | ||
| 2,264 | 2,426 | 2,562 | 2,714 | 2,537 | 2,717 | 2,880 | 3,071 | ||
| 2,297 | 2,461 | 2,602 | 2,759 |
Приложение 4
Квантили распределения Стьюдента
| Число степеней свободы | Уровни значимости р | ||||||
| 0,20 | 0,10 | 0,05 | 0,02 | 0,01 | 0,005 | 0,001 | |
| 3,08 | 6,31 | 12,71 | 31,82 | 63,66 | 127,32 | 636,62 | |
| 1,89 | 2,92 | 4,30 | 6,97 | 9,93 | 14,09 | 31,60 | |
| 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | 7,45 | 12,94 | |
| 1,53 | 2,13 | 2,78 | 3,75 | 4,60 | 5,60 | 8,61 | |
| 1,48 | 2,02 | 2,57 | 3,37 | 4,03 | 4,77 | 6,86 | |
| 1,44 | 1,94 | 2,45 | 3,14 | 3,71 | 4,32 | 5,96 | |
| 1,42 | 1,90 | 2,37 | 3,00 | 3,50 | 4,03 | 5,41 | |
| 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | 3,83 | 5,04 | |
| 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | 3,69 | 4,78 | |
| 1,37 | 1,81 | 2,23 | 2,76 | 3,17 | 3,58 | 4,59 | |
| 1,36 | 1,80 | 2,20 | 2,72 | 3,11 | 3,50 | 4,44 |
Окончание табл.
| Число степеней свободы | Уровни значимости р | ||||||
| 0,20 | 0,10 | 0,05 | 0,02 | 0,01 | 0,005 | 0,001 | |
| 1,36 | 1,78 | 2,18 | 2,68 | 3,06 | 3,43 | 4,32 | |
| 1,35 | 1,77 | 2,16 | 2,65 | 3,01 | 3,37 | 4,22 | |
| 1,34 | 1,76 | 2,15 | 2,62 | 2,98 | 3,33 | 4,14 | |
| 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | 3,29 | 4,07 | |
| 1,34 | 1,75 | 2,12 | 2,58 | 2,92 | 3,25 | 4,02 | |
| 1,33 | 1,74 | 2,11 | 2,57 | 2,90 | 3,22 | 3,97 | |
| 1,33 | 1,73 | 2,10 | 2,55 | 2,88 | 3,20 | 3,92 | |
| 1,33 | 1,73 | 2,09 | 2,54 | 2,86 | 3,17 | 3,88 | |
| 1,33 | 1,73 | 2,09 | 2,53 | 2,85 | 3,15 | 3,85 | |
| 1,32 | 1,72 | 2,08 | 2,52 | 2,83 | 3,14 | 3,82 | |
| 1,32 | 1,72 | 2,07 | 2,51 | 2,82 | 3,12 | 3,79 | |
| 1,32 | 1,71 | 2,07 | 2,50 | 2,81 | 3,10 | 3,77 | |
| 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | 3,09 | 3,75 | |
| 1,32 | 1,71 | 2,06 | 2,48 | 2,79 | 3,08 | 3,73 | |
| 1,32 | 1,71 | 2,06 | 2,48 | 2,78 | 3,07 | 3,71 | |
| 1,31 | 1,70 | 2,05 | 2,47 | 2,77 | 3,06 | 3,69 | |
| 1,31 | 1,70 | 2,05 | 2,47 | 2,76 | 3,05 | 3,67 | |
| 1,31 | 1,70 | 2,04 | 2,46 | 2,76 | 3,04 | 3,66 | |
| 1,31 | 1,70 | 2,04 | 2,46 | 2,75 | 3,03 | 3,65 | |
| 1,30 | 1,68 | 2,02 | 2,42 | 2,70 | 2,97 | 3,55 | |
| 1,30 | 1,67 | 2,00 | 2,39 | 2,66 | 2,91 | 3,46 | |
| 1,29 | 1,66 | 1,98 | 2,36 | 2,62 | 2,86 | 3,37 | |
| ∞ | 1,28 | 1,64 | 1,96 | 2,33 | 2,58 | 2,81 | 3,29 |
Приложение 5
Квантили распределения Пирсона 
| Число степеней свободы, f | Уровни значимости р | ||||||||||
| 0,99 | 0,95 | 0,90 | 0,80 | 0,70 | 0,50 | 0,30 | 0,20 | 0,10 | 0,05 | 0,01 | |
| 0,00016 | 0,0039 | 0,016 | 0,064 | 0,148 | 0,455 | 1,07 | 1,64 | 2,7 | 3,8 | 6,6 | |
| 0,020 | 0,103 | 0,211 | 0,446 | 0,713 | 1,386 | 2,41 | 3,22 | 4,6 | 6,0 | 9,2 | |
| 0,115 | 0,352 | 0,584 | 1,005 | 1,424 | 2,366 | 3,66 | 4,64 | 6,3 | 7,8 | 11,3 | |
| 0,30 | 0,71 | 1,06 | 1,65 | 2,19 | 3,36 | 4,9 | 6,0 | 7,8 | 9,5 | 13,3 | |
| 0,55 | 1,14 | 1,61 | 2,34 | 3,00 | 4,35 | 6,1 | 7,3 | 9,2 | 11,1 | 15,1 | |
| 0,87 | 1,63 | 2,2 | 3,07 | 3,83 | 5,35 | 7,2 | 8,6 | 10,6 | 12,6 | 16,8 | |
| 1,24 | 2,17 | 2,83 | 3,82 | 4,67 | 6,35 | 8,4 | 9,8 | 12,0 | 14,1 | 18,5 | |
| 1,65 | 2,73 | 3,49 | 4,59 | 5,53 | 7,34 | 9,5 | 11,0 | 13,4 | 15,5 | 20,1 | |
| 2,09 | 3,32 | 4,17 | 5,38 | 6,39 | 8,34 | 10,7 | 12,2 | 14,7 | 16,9 | 21,7 | |
| 2,56 | 3,94 | 4,86 | 6,18 | 7,27 | 9,34 | 11,8 | 13,4 | 16,0 | 18,3 | 23,2 | |
| 3,1 | 4,6 | 5,6 | 7,0 | 8,1 | 10,3 | 12,9 | 14,6 | 17,3 | 19,7 | 24,7 | |
| 3,6 | 5,2 | 6,3 | 7,8 | 9,0 | 11,3 | 14,0 | 15,8 | 18,5 | 21,0 | 26,2 | |
| 4,1 | 5,9 | 7,0 | 8,6 | 9,9 | 12,3 | 15,1 | 17,0 | 19,8 | 22,4 | 27,7 | |
| 4,7 | 6,6 | 7,8 | 9,5 | 10,8 | 13,3 | 16,2 | 18,2 | 21,1 | 23,7 | 29,1 | |
| 5,2 | 7,3 | 8,5 | 10,3 | 11,7 | 14,3 | 17,3 | 19,3 | 22,3 | 25,0 | 30,6 | |
| 8,3 | 10,9 | 12,4 | 14,6 | 16,3 | 19,3 | 22,8 | 25,0 | 28,4 | 31,4 | 37,6 | |
| 11,5 | 14,6 | 16,5 | 18,9 | 20,9 | 24,3 | 28,2 | 30,7 | 34,4 | 37,7 | 44,3 | |
| 15,0 | 18,5 | 20,6 | 23,4 | 25,5 | 29,3 | 33,5 | 36,3 | 40,3 | 43,8 | 50,9 |
Приложение 6
Квантили нормального распределения
| р | 1 –р/2 | u1– р /2 | р | 1 – р/2 | u1– р /2 |
| 0,80 | 0,60 | 0,25 | 0,05 | 0,975 | 1,96 |
| 0,50 | 0,75 | 0,67 | 0,04 | 0,980 | 2,05 |
| 0,40 | 0,80 | 0,84 | 0,02 | 0,990 | 2,33 |
| 0,30 | 0,85 | 1,04 | 0,01 | 0,995 | 2,58 |
| 0,25 | 0,875 | 1,15 | 0,005 | 0,9975 | 2,81 |
| 0,20 | 0,90 | 1,28 | 0,002 | 0,999 | 3,09 |
| 0,15 | 0,925 | 1,44 | 0,001 | 0,9995 | 3,29 |
| 0,10 | 0,95 | 1,64 | 0,0001 | 0,99995 | 3,89 |
Здесь р – уровень значимости; u1– р /2 – значение квантиля, соответствующего вероятности (1 – р/2).
Приложение 7
Значения звездного плеча a для различного числа факторов k
и опытов в центре плана n 0
| n 0 | k | |||
| 5* | ||||
| 1,215 | 1,414 | 1,546 | ||
| 1,077 | 1,285 | 1,471 | 1,606 | |
| 1,148 | 1,353 | 1,546 | 1,664 | |
| 1,214 | 1,414 | 1,606 | 1,718 | |
| 1,267 | 1,471 | 1,664 | 1,463 | |
| 1,320 | 1,525 | 1,718 | 1,819 | |
| 1,369 | 1,575 | 1,772 | 1,868 | |
| 1,414 | 1,623 | 1,819 | 1,913 | |
| 1,454 | 1,668 | 1,868 | 1,957 | |
| 1,498 | 1,711 | 1,913 | 2,000 |
* полуреплика, х 5 = х 1 х 2 х 3 х 4.
Приложение 8
Квантили распределения Фишера
| f 2 | f 1 | ||||||||
| 164,4 | 199,5 | 215,7 | 224,6 | 230,2 | 234,0 | 244,9 | 249,0 | 254,3 | |
| 18,5 | 19,2 | 19,2 | 19,3 | 19,3 | 19,3 | 19,4 | 19,5 | 19,5 | |
| 10,1 | 9,6 | 9,3 | 9,1 | 9,0 | 8,9 | 8,7 | 8,6 | 8,5 | |
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | 6,2 | 5,9 | 5,8 | 5,6 | |
| 6,6 | 5,8 | 5,4 | 5,2 | 5,1 | 5,0 | 4,7 | 4,5 | 4,4 | |
| 6,0 | 5,1 | 4,8 | 4,5 | 4,4 | 4,3 | 4,0 | 3,8 | 3,7 | |
| 5,6 | 4,7 | 4,4 | 4,1 | 4,0 | 3,9 | 3,6 | 3,4 | 3,2 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | 3,6 | 3,3 | 3,1 | 2,9 | |
| 5,1 | 4,3 | 3,9 | 3,6 | 3,5 | 3,4 | 3,1 | 2,9 | 2,7 | |
| 5,0 | 4,1 | 3,7 | 3,5 | 3,3 | 3,2 | 2,9 | 2,7 | 2,5 | |
| 4,8 | 4,0 | 3,6 | 3,4 | 3,2 | 3,1 | 2,8 | 2,6 | 2,4 | |
| 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | 3,0 | 2,7 | 2,5 | 2,3 | |
| 4,7 | 3,8 | 3,4 | 3,2 | 3,0 | 2,9 | 2,6 | 2,4 | 2,2 | |
| 4,6 | 3,7 | 3,3 | 3,1 | 3,0 | 2,9 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,7 | 3,3 | 3,1 | 2,9 | 2,8 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,9 | 2,7 | 2,4 | 2,2 | 2,0 |
Окончание табл.
| f 2 | f 1 | ||||||||
| 4,5 | 3,6 | 3,2 | 3,0 | 2,8 | 2,7 | 2,4 | 2,2 | 2,0 | |
| 4,4 | 3,6 | 3,2 | 2,9 | 2,8 | 2,7 | 2,3 | 2,1 | 1,9 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | 1,8 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | 1,8 | |
| 4,3 | 3,4 | 3,1 | 2,8 | 2,7 | 2,6 | 2,2 | 2,0 | 1,8 | |
| 4,3 | 3,4 | 3,0 | 2,8 | 2,6 | 2,5 | 2,2 | 2,0 | 1,7 | |
| 4,2 | 3,4 | 3,0 | 2,7 | 2,6 | 2,4 | 2,1 | 1,9 | 1,7 | |
| 4,2 | 3,3 | 2,9 | 2,7 | 2,6 | 2,4 | 2,1 | 1,9 | 1,6 | |
| 4,2 | 3,3 | 2,9 | 2,7 | 2,5 | 2,4 | 2,1 | 1,9 | 1,6 | |
| 4,1 | 3,2 | 2,9 | 2,6 | 2,5 | 2,3 | 2,0 | 1,8 | 1,5 | |
| 4,0 | 3,2 | 2,8 | 2,5 | 2,4 | 2,3 | 1,9 | 1,7 | 1,4 | |
| 3,9 | 3,1 | 2,7 | 2,5 | 2,3 | 2,2 | 1,8 | 1,6 | 1,3 | |
| ∞ | 3,8 | 3,0 | 2,6 | 2,4 | 2,2 | 2,1 | 1,8 | 1,5 | 1,0 |
МОШЕВ Евгений Рудольфович
Моделирование
химико-технологических процессов
Методические указания
Редактор и корректор И.Н. Жеганина
Лицензия ЛР № 020370
Подписано в печать 8.06.06. Формат 60´90/16.
Набор компьютерный. Объем 3,25.
Тираж 100. Заказ 71/2006
Редакционно-издательский отдел
Пермского государственного технического университета.
Адрес: 614600, Пермь, Комсомольский пр., 29
Отпечатано в Отделе электронных издательских систем ОЦНИТ
Пермского государственного технического университета.
Адрес: 614600, Пермь, Комсомольский пр., 29, к. 113.
