Моделирование
Химико-технологических
Процессов
Методические указания
к выполнению лабораторных работ
Пермь 2006
Составитель – канд. техн. наук Е.Р. Мошев.
УДК 519.7
Математическое моделирование процессов и аппаратов химической технологии: Метод. указания к выполнению лабораторных работ / Сост. Е.Р. Мошев. Перм. гoc. техн. ун-т. – Пермь, 2006. – 52 с.
Дано описание шести лабораторных работ по математическому моделированию химико-технологических процессов. В работах рассмотрены модели идеального перемешивания, идеального вытеснения, ячеечная, ячеечная с рециркуляцией, статистическая и регрессионная. Каждая из работ содержит задачу, решение которой требует самостоятельного составления небольшой компьютерной программы.
Рецензент А.С. Островский, канд. техн. наук
© Пермский государственный
технический университет, 2006
Содержание
Лабораторная работа № 1.......................................................................... 4
Лабораторная работа № 2.......................................................................... 9
Лабораторная работа № 3........................................................................ 14
Лабораторная работа № 4........................................................................ 19
Лабораторная работа № 5........................................................................ 24
Лабораторная работа № 6........................................................................ 36
Приложение 1............................................................................................ 44
Приложение 2............................................................................................ 46
Приложение 3............................................................................................ 47
Приложение 4............................................................................................ 47
Приложение 5............................................................................................ 49
Приложение 6............................................................................................ 49
Приложение 7............................................................................................ 50
Приложение 8............................................................................................ 50
Лабораторная работа № 1
Моделирование работы аппарата
с перемешивающим устройством
Цели работы: ознакомиться с моделью идеального перемешивания (ИП); научиться определять среднее время пребывания потока в аппарате по экспериментальной функции отклика на импульсное возмущение; освоить практическое применение модели ИП для исследования работы аппарата с мешалкой; решить приведенную задачу.
Краткие теоретические сведения
Модель ИП является теоретической моделью с идеализированной структурой потока. В соответствии с ней принимается, что поступающий в аппарат поток вследствие полного перемешивания частиц среды мгновенно распределяется по всему объему. При этом концентрация распределенного вещества во всех точках аппарата одинакова и равна концентрации на выходе.
Схематично данную модель можно представить следующим образом:

 .
.
Модель ИП наиболее адекватно воспроизводит структуру потока в аппаратах с мешалками (рис. 1), имеющими эллиптические или полусферические днища, соотношение высоты и диаметра корпуса, близкое к единице, снабженные отражательными перегородками.
Математическое описание модели ИП имеет вид
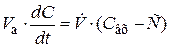 или или  , ,
| (1) |
где 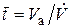 – среднее время пребывания потока в аппарате;
– среднее время пребывания потока в аппарате; 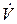 – объёмный расход потока; Va – объём аппарата. Свх, С и Свых – концентрация вещества на входе в аппарат, в аппарате и на выходе из аппарата соответственно.
– объёмный расход потока; Va – объём аппарата. Свх, С и Свых – концентрация вещества на входе в аппарат, в аппарате и на выходе из аппарата соответственно.
В условиях стационарного режима и отсутствия каких-либо превращений вещества Свх = С = Свых.
Отклики модели на типовые возмущения представлены на рис. 2.

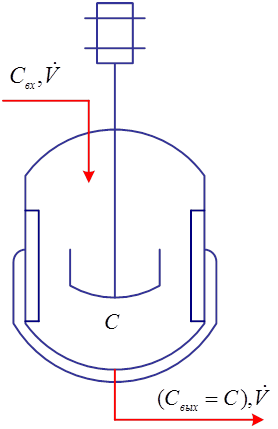
Рис. 1. Принципиальная схема аппарата
с мешалкой
|
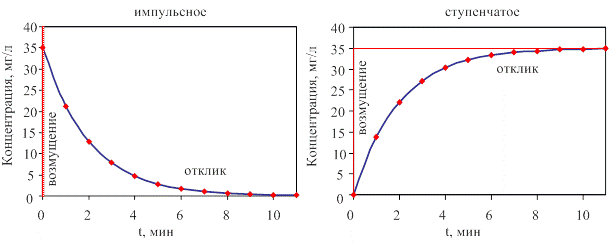
Рис. 2. Отклики модели ИП на типовые возмущения
Решения модели:
Импульсное возмущение
Для граничных условий Свх = 0 и Свых = Сн = G/Va в момент времени t = 0,
 , (2) , (2)
|
где t – текущее время; Сн – начальная концентрация индикатора в потоке в момент времени t = 0; G – масса индикатора, введенного в аппарат.
Ступенчатое возмущение
Для граничных условий Свых= 0 при t = 0; Свх = const.
 . .
| (3) |
Основным параметром модели ИП является среднее время пребывания 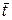 , которое в случае импульсного возмущения определяется по формуле
, которое в случае импульсного возмущения определяется по формуле
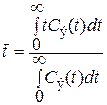 , (4) , (4)
|
где 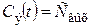 – экспериментальное значение функции отклика.
– экспериментальное значение функции отклика.
Использование полученной функции отклика в натуральных значениях координат С э(t) – t не всегда является удобным для расчетов, поэтому кривую отклика обычно приводят к безразмерному виду С(θ) – θ и называют С-кривой. Здесь θ– безразмерное время, равное  , а С(θ) – безразмерная концентрация, равная
, а С(θ) – безразмерная концентрация, равная  , где
, где  . Безразмерная концентрация связана со средним временем пребывания и экспериментальным значением функции отклика
. Безразмерная концентрация связана со средним временем пребывания и экспериментальным значением функции отклика 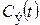 следующей зависимостью:
следующей зависимостью:
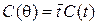 , (5) , (5)
|
где выражение
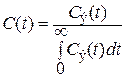 (6) (6)
|
задает нормированную кривую отклика.
Таким образом, С-кривая является характеристикой распределения элементов потока по времени их пребывания в аппарате.
При практическом определении среднего времени пребывания по экспериментальной С-кривой знаки интегралов в выражении (4) заменяются на знаки суммы и посредством суммирования (см. приложение 1) определяется  .
.
Задача
Перед ремонтом реактор, представляющий собой аппарат непрерывного действия с перемешивающим устройством (см. рис. 1), необходимо промыть от находящегося в нем раствора, который содержит токсичный компонент. Условия производства таковы, что промывку можно осуществлять только путем непрерывной подачи чистого растворителя при включенном перемешивающем устройстве (ступенчатое возмущение с понижением концентрации индикатора от текущего значения до нуля). Определить необходимое время промывки реактора из условия, что концентрация токсичного компонента на выходе из реактора не должна превышать 1 кг/м3.
Ход работы
1. Ознакомиться с кратким изложением теории.
2. По результатам испытания аппарата импульсным методом (табл. 1) определить среднее время пребывания потока в аппарате (см. приложение 1) и построить кривую отклика в безразмерных координатах С(θ) – θ.
3. Для условий задачи посредством решения уравнения (1) получить в интегральной форме зависимость концентрации токсичного компонента на выходе из аппарата от времени промывания.
4. Используя данные табл. 2 и результаты выполнения п. 3 графическим способом определить время промывки соответствующее условию задачи.
5. Используя результаты расчета среднего времени пребывания построить кривую отклика на ступенчатое возмущение (для условий Свых = 0 при t = 0; Свх = const = С вых0) и определить время, в течение которого концентрация вещества в аппарате достигнет значения (С вх – 1) кг/м3.
6. Написать вывод по решению задачи.
Таблица 1
Результаты испытания аппарата импульсным методом
| № варианта | Концентрация индикатора на выходе потока из аппарата С вых, кг/м3 | |||||||||
| 0,3 | ||||||||||
| Время измерения концентрации t, мин | ||||||||||
| 1,5 | 4,5 | 7,5 | 10,5 | 13,5 | ||||||
| 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | ||||||
| 3,5 | 10,5 | 17,5 | 24,5 | 31,5 | ||||||
| 4,5 | 13,5 | 22,5 | 31,5 | 40,5 | ||||||
Таблица 2
Начальная концентрация компонента на выходе потока из аппарата
| № вар. | ||||||||||||||||||||||
| С вых0 | ||||||||||||||||||||||
Здесь С вых0 – соответствующая номеру варианта концентрация токсичного компонента на выходе потока из аппарата в момент начала промывки (t = 0), кг/м3.
Лабораторная работа № 2
Моделирование работы теплообменника
Типа труба в трубе
Цели работы: ознакомиться с моделью идеального вытеснения (ИВ); освоить практическое применение модели ИВ для исследования процесса теплообмена в теплообменнике типа труба в трубе; решить приведенную задачу.
Краткие теоретические сведения
Поскольку теплообменники являются наиболее распространенными и необходимыми элементами различных технологических и энергетических установок, то оптимизация их работы представляется чрезвычайно актуальной задачей. Существующие методики расчета теплообменных аппаратов подразумевают осредненные характеристики (средние скорость, температура, коэффициент теплопередачи и т.д.) и не всегда позволяют спроектировать аппарат оптимальной конструкции. Одним из путей повышения точности проектирования является использование методов математического моделирования на основе типовых моделей химической технологии.
В теплообменнике типа труба в трубе структура потока наиболее адекватно может быть воспроизведена моделями ИВ и диффузионной.
Модель ИВ является теоретической моделью с идеализированной структурой движущегося потока. В соответствии с ней принимается поршневое течение потока без продольного перемешивания при равномерном распределении концентрации вещества в направлении, перпендикулярном его движению. Среднее время пребывания всех частиц в системе одинаково и определяется как
 или или 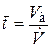 , (1) , (1)
|
где  – среднее время пребывания потока в аппарате; L – длина аппарата; W – скорость потока в аппарате; Va – объем аппарата;
– среднее время пребывания потока в аппарате; L – длина аппарата; W – скорость потока в аппарате; Va – объем аппарата; 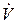 – объемный расход потока.
– объемный расход потока.
Наиболее близкими к модели ИВ являются трубчатые реакторы, теплообменники и другие аппараты с отношением L/d > 20 при Re > 2320.
Принципиальная схема модели ИВ представлена на рис. 1.
Для стационарных условий и при отсутствии каких-либо превращений в аппарате Свх = Свых = С.
Математическое описание модели ИВ имеет вид
 . (2) . (2)
|
Отклики модели на типовые возмущения приведены на рис. 2.
Решение модели, удовлетворяющее начальному условию С (0, z) = = С н(z) при t =0, 0 < z < L и граничному С (t, 0) = С вх(t) при z = 0, t > 0, есть
 , (3) , (3)
|
где Сн – концентрация в аппарате в начальный момент времени.


Рис. 1. Принципиальная схема модели ИВ: С, Свх, Свых – концентрации вещества текущая, на входе и выходе соответственно; t – текущее время; z – координата, вдоль которой перемещается поток со скоростью W; F – площадь поперечного сечения потока
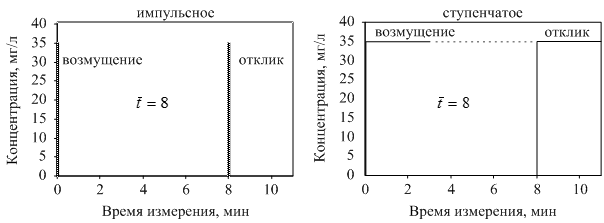
Рис. 2. Отклики модели ИВ на типовые возмущения
Из решений системы следует, что любое возмущение на входе повторяется на выходе через время, равное среднему времени пребывания 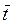 .
.
Рассмотрим использование модели ИВ на примере теплообменника типа труба в трубе (рис. 3), в котором осуществляется нагрев воды конденсирующимся паром. На основании уравнения теплового баланса для слоя с элементарной толщиной dx изменение количества тепла, переносимого хладоагентом, равно количеству тепла, передаваемого паром через поверхность теплопередачи,
 (4)
(4)
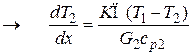 , ,
|

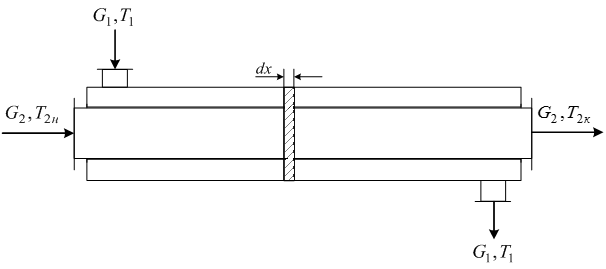
Рис. 3. Принципиальная схема теплообменника: G 1 и G 2 – массовый расход пара и хладоагента; Т 1 – температура пара и конденсата; Т 2н, Т 2к – начальная и конечная температура хладоагента соответственно
где w 2 – скорость течения хладоагента в трубном пространстве; S 2 – площадь поперечного сечения внутренней трубы; r2 – удельная плотность хладоагента; G 2 = w 2 S 2r2– массовый расход хладоагента; cp 2 – удельная теплоемкость хладоагента; K – коэффициент теплопередачи; T 2 – текущая температура хладоагента; х – расстояние от входа в теплообменник; F = П dx – поверхность теплопередачи в элементарном объеме; П – смоченный периметр.
Интегрируя уравнение (4), получим зависимость изменения температуры хладоагента по длине теплообменника

|
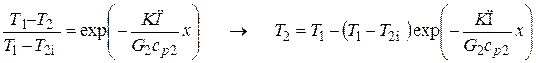 . (5) . (5)
|
Задача
Путем численного моделирования определить: минимальную поверхность теплообменника типа труба в трубе (рис. 3), необходимую для нагревания хладоагента до заданной температуры, и температуру горячего теплоносителя на выходе из аппарата. Исходные данные представлены в таблице. Диаметр внутренней и внешней труб принять соответственно 0,025 и 0,05 (м), толщиной стенки труб пренебречь. Режим течения теплоносителей турбулентный. Длины прямых участков теплообменника превышают его диаметр более чем в 20 раз.
Ход работы
1. Ознакомиться с кратким изложением теории.
2. По аналогии с уравнением (4) получить систему из 2 дифференциальных уравнений, включающую зависимости изменения температур теплоносителей по длине теплообменника. Cоставить программу для решения системы методом Эйлера (см. приложение 2).
3. Используя таблицу исходных данных, путем проведения вычислительного эксперимента определить:
– оптимальный шаг решения дифференциального уравнения (шаг следует считать оптимальным, если расхождение между длинами теплообменника, определенными по дифференциальному уравнению и через осредненные характеристики по уравнению  не будет превышать 0,1 м, где
не будет превышать 0,1 м, где 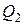 – передаваемое хладоагенту количество тепла;
– передаваемое хладоагенту количество тепла; 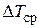 –средняя разность температур теплоносителей);
–средняя разность температур теплоносителей);
– минимальную поверхность теплообмена, необходимую для нагревания хладоагента до заданной температуры;
– температуру горячего теплоносителя на выходе из теплообменника.
4. Построить график изменения температуры теплоносителей по длине теплообменника.
5. Написать вывод по решению задачи.
Исходные данные для расчета
| № вар. | ||||||||||
| Т2н, °С | ||||||||||
| Т2к, °С | ||||||||||
| w2, м/с | 0,5 | 0,7 | 1,0 | 1,2 | 1,4 | 1,5 | 1,7 | 1,8 | 1,9 | 2,0 |
| r2,кг/м3 | ||||||||||
| ср2, Дж/(кг·гр) | ||||||||||
| Т1н, °С | ||||||||||
| w1, м/с | 0,5 | 0,7 | 1,0 | 1,2 | 1,4 | 1,5 | 1,7 | 1,8 | 1,9 | 2,0 |
| r1, кг/м3 | ||||||||||
| ср1, Дж/(кг·гр) | ||||||||||
| К, Вт/(м2·гр) |
Лабораторная работа № 3






